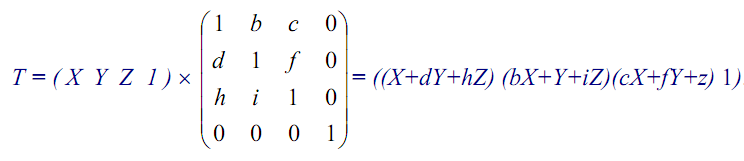7. Элементарные (базовые) и комбинированные операции в пространстве.

По аналогии с вариантом для плоскости для унификации матричных операций введем дополнительную координату, т.е. будем представлять координаты (x, y, z) точек объектов пространства в виде (x, y, z, 1). Данная форма является частным случаем более общего представления, используемого в проективной геометрии - (x, y, z, h). Рабочее трехмерное пространство представляет собой пространство проективной геометрии при H = const, поэтому перед началом работы необходимо определить величину H. Для упрощения дальнейших вычислений выбирается H = 1. Преобразования в подобной системе координат возможны только в том случае, если все координаты имеют одинаковую размерность, т.е. пространство является однородным, поэтому такая система координат называется системой однородных координат. Обобщая двумерную матрицу преобразований на трехмерный случай, получим:

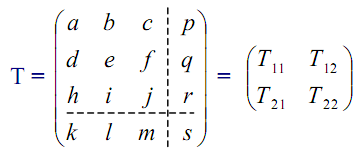
Четыре подматрицы Т11, T21, T12, T22 определяют следующие виды преобразований в трехмерном пространстве:

1) Т11 определяет линейные преобразования частичного масштабирования, вращения и линейной трансформации;

2) Т21 определяет преобразование переноса геометрических объектов;

3) Т12 отвечает за построение перспективы;

4) Т22 отвечает за глобальный масштаб изображения.

Результатом воздействия матрицы преобразований Т на трехмерный геометрический объект (X Y Z 1) является новый геометрический объект, который, в общем случае, может иметь следующий вид:

(X' Y' Z' H') = (X Y Z 1) × T.

Чтобы новый объект располагался в том же пространстве, что и исходный, необходимо выполнить операцию нормализации:

(X' Y' Z' H') norm⇒ ( X'/H' Y'/H' Z'/H' 1) = (X* Y* Z* 1)

Таким образом, полное преобразование в трехмерном пространстве получается путем умножения матрицы координат исходного объекта на матрицу преобразований Т с последующей ее нормализацией. При помощи матрицы Т можно осуществить операции переноса, масштабирования, отображения, вращения, линейной трансформации и построение различного вида перспектив. Часть из этих операций может быть совмещена, а другие операции должны выполняться последовательно, например, трансформация и вращение. Возможность совмещения операций определяется отсутствием в их матрицах преобразований общих элементов. Например, операции переноса и вращения определяются элементами различных подматриц (соответственно Т11 и Т21), то есть ненулевые элементы не перекрываются, поэтому их

Перенос в трехмерном пространстве. Операция переноса реализуется при помощи следующей матрицы:

Масштабирование по осям координат. Диагональные элементы подматрицы Т11 позволяют произвести частичное масштабирование по координатным осям x, y, z.

(X Y Z 1 ) ×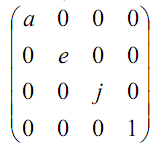 = (aX eY jZ 1)

Примечание. Обратите внимание на то, что коэффициенты частичного масштабирования a, e, j определяют увеличение размеров геометрических объектов, а коэффициент общего масштаба s определяет уменьшение размеров.

Вращение вокруг осей координат. Вращение вокруг осей координат в пространстве описывается по аналогии с вращением в плоскости вокруг начала системы координат (см. предыдущую тему). Пространственное вращение вокруг оси OZ совпадает с вращением вокруг начала системы координат в плоскости XOY (вариант, рассмотренный в предыдущей теме). Пространственное вращение вокруг оси OX будет соответствовать вращению вокруг начала системы координат в плоскости YOZ, а вокруг оси OY - в плоскости XOZ. С математической точки зрения вращение вокруг одной из координатных осей имеет место при равенстве определителя матрицы Т11 единице (det T11 = 1). Таким образом, для случая вращения вокруг оси OX матрица преобразований имеет вид:

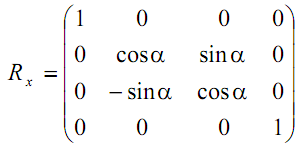а матрицы, описывающие повороты вокруг осей OY, OZ будут выгля-

деть следующим образом:

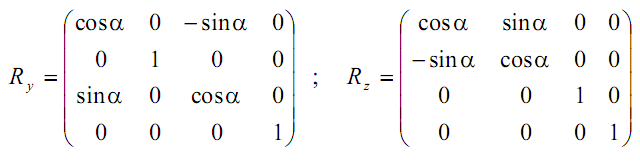
Примечание. Так как вращение описывается при помощи матричной операции умножения, которая не является коммутативной, то порядок вращения графического объекта будет влиять на конечный результат.

Отображения в пространстве. Зеркальные отображения реализуются для отображения относительно координатных плоскостей. Для отображения без изменения масштаба необходимо, чтобы диагональные элементы матрицы Т11 были по модулю равны единице, а определитель равнялся минус единице.

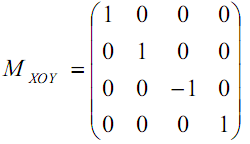
Аналогично определяется матрица для зеркального отображения относительно плоскостей XOZ, YOZ. Отображение относительно произвольных плоскостей можно получить при помощи комбинации операций переноса, вращения и отображения.

Для выполнения данной последовательности шагов, включающей прямые и обратные преобразования, используются операции преобразования, которое называется преобразованием конгруэнтности. Преобразование конгруэнтности - последовательность прямых и обратных преобразований:

T=A×B×C×…×X×…×CТ×BТ×AТ или T=AТ×BТ×CТ×…×X×…×C×B×AПространственная линейная трансформация. Недиагональныеэлементы матрицы Т11 определяют линейную трансформацию геометрического объекта в трехмерном пространстве. Например: