Линейно зависимые и линейно независимые системы векторов

Рассмотрим несколько векторов  .

Линейной комбинацией данных векторов называется любой вектор вида  , где   - некоторые числа. Числа   называются коэффициентами линейной комбинации. Говорят также, что в этом случае   линейно выражается через данные векторы  , т.е. получается из них с помощью линейных действий.

Например, если даны три вектора   то в качестве их линейной комбинации можно рассматривать векторы: 

Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.

Векторы   называются линейно зависимыми, если существуют такие числа , не все равные нулю, что  . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.

В противном случае, т.е. когда соотношение   выполняется только при  , эти векторы называются линейно независимыми.

Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Доказательство:

1. Действительно, пусть имеем два коллинеарных вектора   и 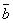 . Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация 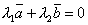  при любых λ₁ и λ₂, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например, 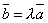 . Но отсюда  , а это и означает линейную зависимость векторов   и  .

2. Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы   и   линейно зависимы. Тогда найдутся числа λ₁ и λ₂ такие, что  , причём, например, λ₂ ≠ 0. Тогда 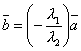 , т.е. векторы коллинеарны.

Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны.

Аналогично можно доказать следующую теорему.

Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Доказательство.

1. Пусть три вектора   линейно зависимы, т.е. 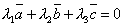 , где, например, λ₃ ≠ 0. Тогда  .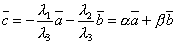

Отнесём векторы   и   к одному началу и проведём через них плоскость. Тогда   и   будут лежать в той же плоскости, а потому и их сумма, т.е.   будет лежать в той же плоскости, т.е.   – компланарны.

2. Пусть теперь векторы   – компланарны. Тогда они будут лежать в одной плоскости. Отнесём все три вектора к одному началу.

Если векторы   и   не коллинеарны, то очевидно, вектор   можно предствить в виде  . Действительно из рисунка видно, что  , где   и  , а значит найдутся числа   и  такие, что  .

Е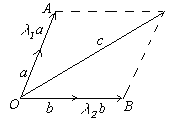 сли же вектор   коллинеарен вектору  , то один из них линейно выражен через другой, т.е.  . Что и требовалось доказать.

Таким образом, три некомпланарных вектора всегда линейно независимы. Кроме того, можно показать, что каждые четыре вектора линейно зависимы.

Билет 10.

СПОСОБЫ ГРАФИЧЕСКОГО ЗАДАНИЯ ПРЯМОЙ ЛИНИИ

Для определения положения прямой в пространстве существуют следующие методы:

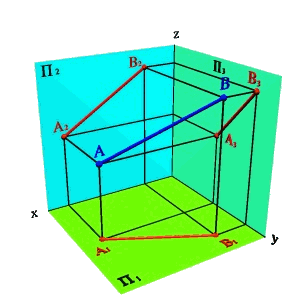
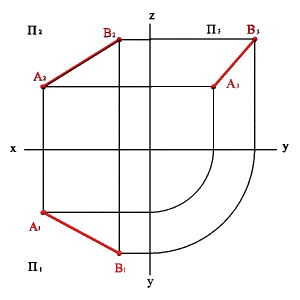
1.Двумя точками (а и в).

 Рассмотрим две точки в пространстве А и В (рис. 15). Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка[AB] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: 

[A₁B₁]<[AB]; [A₂B₂]<[AB]; [A₃B₃]<[AB].

а) модель		б) эпюр
Рисунок 15.Определение положения прямой по двум точкам

Обозначим углы между прямой и плоскостями проекций через α- с плоскостью П₁, β- с плоскостью П₂, γ- с плоскостью П₃ и тогда получим:

|А₁В₁|=|AB|cos 

|A₂B₂|=|AB|cos

|A₃B₃|=|AB|cos .

Частный случай |A₁B₁|=|A₂B₂|=|A₃B₃| при таком соотношении прямая образует с плоскостями проекций равные между собой углы===35⁰, при этом каждая из проекций расположена под углом 45⁰ к соответствующим осям проекций.