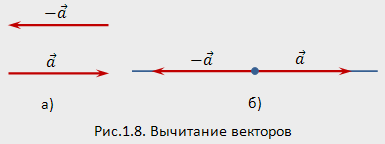
Вычитание векторов

Вектор   называется противоположным вектору  , если их сумма равна нулевому вектору:  . Противоположный вектор   имеет длину  , коллинеарен и противоположно направлен вектору   (рис.1.8,а,б). Нулевой вектор является противоположным самому себе.

Разностью векторов   и   называется сумма вектора   с вектором  , противоположным вектору  :

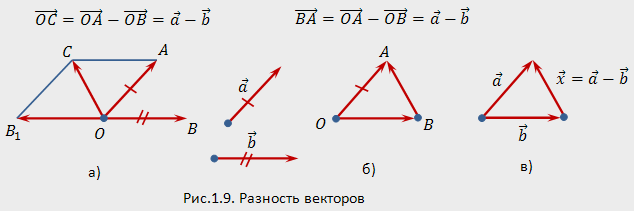
Для нахождения разности векторов   и   приложим к произвольной точке   векторы  , а также вектор  , противоположный вектору   (рис.1.9,а). Искомую разность находим по правилу параллелограмма:

Для нахождения разности проще использовать правило треугольника (рис. 1.9,6). Для этого прикладываем к произвольной точке   векторы  . Вектор   при этом равен искомой разности  .

Вычитание векторов — действие, обратное сложению — можно определить также следующим образом: разностью векторов   и  называется такой вектор  , который в сумме с вектором   дает вектор   (рис.1.9,в), т.е. разность   — это решение уравнения  .

Пример 1.2. Для векторов на рис. 1.6 найти следующие суммы и разности:

Решение. Учитывая равенство  , получаем по правилу треугольника  .

Поскольку   и  , то  .

По правилу параллелограмма  .

Так как   и  , находим 

Умножение вектора на число

Произведением ненулевого вектора а на действительное число   называется вектор  , удовлетворяющий условиям:

1) длина вектора   равна  , т.е.  ;

2) векторы   и   коллинеарные  ;

3) векторы   и   одинаково направлены, если  , и противоположно направлены, если  .

Произведение нулевого вектора на любое число   считается (по определению) нулевым вектором:  ; произведение любого вектора на число нуль также считается нулевым вектором:  . Из определения произведения следует, что:

а) при умножении на единицу   вектор не изменяется:  ;

б) при умножении вектора на   получается противоположный вектор:  ;

в) деление вектора на отличное от нуля число   сводится к его умножению на число  , обратное  .

г) при делении ненулевого вектора   на его длину, т.е. при умножении   на число   получаем единичный вектор, одинаково направленный с вектором  .

Действительно, длина вектора   равна единице:  .

Вектор   коллинеарен и одинаково направлен с вектором  , так как  ;

д) при умножении единичного вектора на число   получаем коллинеарный ему вектор, длина которого равна  .

На рис.1.10 изображены векторы, получающиеся в результате умножения данного вектора   на   и  , а также противоположный вектор  .

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов   и любых действительных чисел   справедливы равенства:

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.