Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида  ).

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) =g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку   теорему Коши. По этой теореме получим:

,

но f(a) = g(a) = 0, поэтому  .

Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:

 для конечного предела и

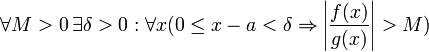 для бесконечного,

что является определением предела отношения функций.

[Править]Отношение бесконечно больших

Докажем теорему для неопределённостей вида  .

Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:

.

Зафиксируем t из отрезка   и применим теорему Коши ко всем x из отрезка  :

, что можно привести к следующему виду:

.

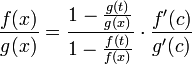Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α:

.

Получили, что отношение функций представимо в виде (1 + β)(A + α), и 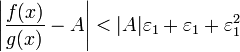 . По любому данному ε можно найти такое ε₁, чтобы модуль разности отношения функций и A был меньше ε, значит, предел отношения функций действительно равен A.

Если же предел A бесконечен (допустим, он равен плюс бесконечности), то

.

В определении β будем брать  ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда  .

Парадокс заключается в том, что любая степень единицы равна самой единице: 1a = 1. Следовательно, и  . Таким образом, это не должно быть неопределённостью.

Так почему же это является неопределённостью? Править

По правилу Лопиталя  . Но поскольку   (по условию), то одним из множителей второго предела является  , что уже говорит о том, что вычислить этот предел невозможно. Таким образом,   является неопределённостью, и это доказано.