
- •2 Билет.
- •3 Билет.
- •Алгоритм Описание
- •Вычитание векторов
- •Умножение вектора на число
- •Свойства линейных операций над векторами
- •Линейные комбинации векторов
- •§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
- •§ 2. Скалярное произведение векторов.
- •§ 3. Векторное произведение векторов.
- •§4. Смешанное произведение векторов.
- •В координатной форме
- •[Править]Обозначения
- •[Править]Свойства коллинеарности
- •Линейно зависимые и линейно независимые системы векторов
- •1.Двумя точками (а и в).
- •2. Двумя плоскостями (; ).
- •3. Двумя проекциями.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
- •Расстояние от точки до прямой
- •Угол между прямыми на плоскости
- •Уравнение плоскости
- •Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.
- •Расстояние от точки до прямой
- •Взаимное расположение двух плоскостей (формулировки и примеры)
- •Угол между плоскостями
- •Прямая в пространстве
- •Числовые последовательности
- •Арифметические действия над числовыми последовательностями
- •Ограниченные и неограниченные последовательности
- •Бесконечно большие и бесконечно малые последовательности
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •Оновные свойства бесконечно малых последовательностей
- •Определения
- •[Править]Промежутки монотонности
- •[Править]Примеры
- •Способы определения
- •[Править]Свойства
- •Теорема о вложенных отрезках
- •Односторонний предел по Гейне
- •[Править]Односторонний предел по Коши
- •Теоремы о пределах
- •Второй замечательный предел
- •Исчисление бесконечно малых и больших
- •[Править]Бесконечно малая величина
- •[Править]Бесконечно большая величина
- •[Править]Свойства бесконечно малых
- •[Править]Сравнение бесконечно малых
- •[Править]Определения
- •[Править]Примеры сравнения
- •Определение непрерывности функции
- •Арифметические действия над непрерывными функциями
- •Определение
- •[Править]Существование
- •[Править]Примеры
- •[Править]Свойства
- •Понятие производной
- •Геометрический смысл производной
- •Производные и дифференциалы высших порядков
- •Дифференцируемость
- •[Править]Замечания
- •Дифференцирование функций, заданных параметрически
- •Следствие
- •Доказательство Лагранжа
- •Отношение бесконечно малых
- •[Править]Отношение бесконечно больших
- •Так почему же это является неопределённостью? Править
Геометрический смысл производной
Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение D x№ 0, причем x+D x О (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+D x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+D x,f(x+D x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (D x).
Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x® 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.

Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел limD x® 0f (D x) = f 0, который равен углу, образованному касательной с положительным направлением оси OX.
ункция y=f(x) называется дифференцируемой в
некоторой точке x0,
если она имеет в этой точке определенную
производную, т.е. если предел
отношения ![]() существует
и конечен.
существует
и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом,из дифференцируемости функции следует ее непрерывность.
Доказательство.
Если ![]() ,
то
,
то
![]() ,
,
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда
Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).
Р ассмотрим
на рисунке точки а,
b, c.
ассмотрим
на рисунке точки а,
b, c.
В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точкеA графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к1 и к2. Такой тип точек называют угловыми точками.
В
точке b при
Δx→0
отношение
является
знакопостоянной бесконечно большой
величиной ![]() .
Функция имеет бесконечную производную.
В этой точке график имеет вертикальную
касательную. Тип точки – "точка
перегиба" cвертикальной касательной.
.
Функция имеет бесконечную производную.
В этой точке график имеет вертикальную
касательную. Тип точки – "точка
перегиба" cвертикальной касательной.
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.
Билет 39.
Дифференциал — это малое изменение величины в математическом выражении вследствие такого же незначительного изменения переменной.
Приближённые вычисления с помощью дифференциала
Формулу ![]() задающую
определение дифференциала, можно
записать в виде приближённого
равенства
задающую
определение дифференциала, можно
записать в виде приближённого
равенства ![]() если
считать (при малых
если
считать (при малых ![]() )
значение бесконечно малой величины
)
значение бесконечно малой величины ![]() много
меньшим, чем
.
Перенося
много
меньшим, чем
.
Перенося ![]() в
правую часть, получаем:
в
правую часть, получаем: ![]() где
где![]() .
С учётом выражения дифференциала через
частные производные, находим, что
.
С учётом выражения дифференциала через
частные производные, находим, что 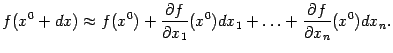 Эту
формулу можно применять для приближённого
вычисления значений функции
в
точках
,
если известны значения
и
её частных производных
Эту
формулу можно применять для приближённого
вычисления значений функции
в
точках
,
если известны значения
и
её частных производных ![]() в
точке
в
точке ![]() .
Пример 7 . 23
Пусть требуется приближённо вычислить
значение
.
Пример 7 . 23
Пусть требуется приближённо вычислить
значение ![]() Рассмотрим
функцию
Рассмотрим
функцию ![]() и
будем трактовать числа
и
будем трактовать числа![]() как
малые отклонения на
как
малые отклонения на![]() ,
, ![]() ,
, ![]() от
"круглых" значений
от
"круглых" значений ![]() .
Поскольку
.
Поскольку 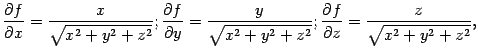 то
дифференциал функции равен
то
дифференциал функции равен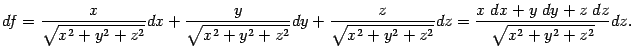 Значение
функции в точке
Значение
функции в точке ![]() равно
равно ![]() значения
частных производных равны
значения
частных производных равны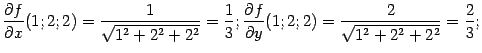
 Поэтому
Поэтому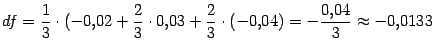 и
и![]()
Билет 40.
Таблица производных. Табличные производные."таблица производный"-да, к сожалению, именно так их и ищут в интернете |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная натурального логарифма функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила дифференцирования. Производная произведения. Производная частного. Производная сложной функции. |
|
Производная произведения (функции) на постоянную: |
|
Производная суммы (функций): |
|
Производная произведения (функций): |
|
Производная частного (функций): |
|
Производная сложной функции: |
|
Билет 42.


 Производная
косеканса
Производная
косеканса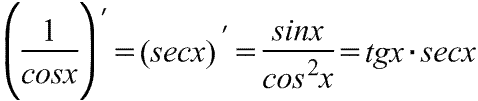 Производная
секанса
Производная
секанса Производная
арксинуса
Производная
арксинуса Производная
арккосинуса
Производная
арккосинуса Производная
арксинуса
Производная
арксинуса Производная
арккосинуса
Производная
арккосинуса Производная
арктангенса
Производная
арктангенса Производная
арккотангенса
Производная
арккотангенса Производная
арксеканса
Производная
арксеканса Производная
арккосеканса
Производная
арккосеканса Производная
арксеканса
Производная
арксеканса Производная
арккосеканса
Производная
арккосеканса Производная
гиперболического синуса
Производная
гиперболического синуса Производная
гиперболического синуса в английской
версии
Производная
гиперболического синуса в английской
версии Производная
гиперболического косинуса
Производная
гиперболического косинуса Производная
гиперболического косинуса в английской
версии
Производная
гиперболического косинуса в английской
версии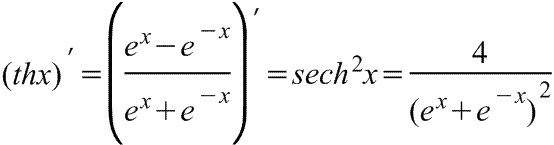 Производная
гиперболического тангенса
Производная
гиперболического тангенса Производная
гиперболического котангенса
Производная
гиперболического котангенса Производная
гиперболического секанса
Производная
гиперболического секанса Производная
гиперболического косеканса
Производная
гиперболического косеканса

