
- •2 Билет.
- •3 Билет.
- •Алгоритм Описание
- •Вычитание векторов
- •Умножение вектора на число
- •Свойства линейных операций над векторами
- •Линейные комбинации векторов
- •§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
- •§ 2. Скалярное произведение векторов.
- •§ 3. Векторное произведение векторов.
- •§4. Смешанное произведение векторов.
- •В координатной форме
- •[Править]Обозначения
- •[Править]Свойства коллинеарности
- •Линейно зависимые и линейно независимые системы векторов
- •1.Двумя точками (а и в).
- •2. Двумя плоскостями (; ).
- •3. Двумя проекциями.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
- •Расстояние от точки до прямой
- •Угол между прямыми на плоскости
- •Уравнение плоскости
- •Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.
- •Расстояние от точки до прямой
- •Взаимное расположение двух плоскостей (формулировки и примеры)
- •Угол между плоскостями
- •Прямая в пространстве
- •Числовые последовательности
- •Арифметические действия над числовыми последовательностями
- •Ограниченные и неограниченные последовательности
- •Бесконечно большие и бесконечно малые последовательности
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •Оновные свойства бесконечно малых последовательностей
- •Определения
- •[Править]Промежутки монотонности
- •[Править]Примеры
- •Способы определения
- •[Править]Свойства
- •Теорема о вложенных отрезках
- •Односторонний предел по Гейне
- •[Править]Односторонний предел по Коши
- •Теоремы о пределах
- •Второй замечательный предел
- •Исчисление бесконечно малых и больших
- •[Править]Бесконечно малая величина
- •[Править]Бесконечно большая величина
- •[Править]Свойства бесконечно малых
- •[Править]Сравнение бесконечно малых
- •[Править]Определения
- •[Править]Примеры сравнения
- •Определение непрерывности функции
- •Арифметические действия над непрерывными функциями
- •Определение
- •[Править]Существование
- •[Править]Примеры
- •[Править]Свойства
- •Понятие производной
- •Геометрический смысл производной
- •Производные и дифференциалы высших порядков
- •Дифференцируемость
- •[Править]Замечания
- •Дифференцирование функций, заданных параметрически
- •Следствие
- •Доказательство Лагранжа
- •Отношение бесконечно малых
- •[Править]Отношение бесконечно больших
- •Так почему же это является неопределённостью? Править
Односторонний предел по Гейне
Ч
 исло
исло 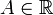 называется правосторонним
пределом (правым
пределом, пределом
справа)
функции
называется правосторонним
пределом (правым
пределом, пределом
справа)
функции 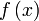 в
точке
в
точке  ,
если для всякой последовательности
,
если для всякой последовательности  ,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции 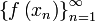 сходится
к числу
.
сходится
к числу
.
Ч
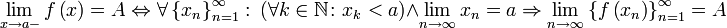 исло
называется левосторонним
пределом (левым
пределом, пределом
слева)
функции
в
точке
,
если для всякой последовательности
,
состоящей из точек, меньших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
сходится
к числу
.[1]
исло
называется левосторонним
пределом (левым
пределом, пределом
слева)
функции
в
точке
,
если для всякой последовательности
,
состоящей из точек, меньших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
сходится
к числу
.[1]
[Править]Односторонний предел по Коши
Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякого положительного числа
 отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число  такое,
что для всех
точек
такое,
что для всех
точек 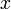 из интервала
из интервала 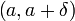 справедливо неравенство
справедливо неравенство  .
.
![]()
Ч
 исло
называется левосторонним
пределом (левым
пределом, пределом
слева)
функции
в
точке
,
если для всякого положительного
числа
отыщется
отвечающее ему положительное
число
такое,
что для всех точек
из
интервала
исло
называется левосторонним
пределом (левым
пределом, пределом
слева)
функции
в
точке
,
если для всякого положительного
числа
отыщется
отвечающее ему положительное
число
такое,
что для всех точек
из
интервала  справедливо
неравенство
.[1]
справедливо
неравенство
.[1]
Билет 30.
Теоремы о пределах
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
![]() .
.
Доказательство.
Проведем доказательство для двух
слагаемых, так как для любого числа
слагаемых оно проводится так же.
Пусть ![]() .Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
.Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то
![]() .
.
Пример. ![]() .
.
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
![]() .
.
Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть
величина постоянная. Функция bβ
+ c α + αβ на
основании свойств бесконечно малых
функций есть величина бесконечно малая.
Поэтому ![]() .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
![]() .
.
Следствие 2. Предел степени равен степени предела:
![]() .
.
Пример.![]() .
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
 .
.
Доказательство.
Пусть ![]() .
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α,
β –
бесконечно малые. Рассмотрим частное
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α,
β –
бесконечно малые. Рассмотрим частное
![]() .
.
Дробь ![]() является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
Примеры.
 .
. .
.Рассмотрим
 .
При x→1 числитель
дроби стремится к 1, а знаменатель
стремится к 0. Но так как
.
При x→1 числитель
дроби стремится к 1, а знаменатель
стремится к 0. Но так как  ,
т.е.
,
т.е.  есть
бесконечно малая функция при x→1,
то
есть
бесконечно малая функция при x→1,
то  .
.
Т еорема
4. Пусть
даны три функции f(x),
u(x) и v(x),
удовлетворяющие неравенствам u(x)≤f(x)≤
v(x).
Если функции u(x) и v(x) имеют
один и тот же предел при x→a (или x→∞),
то и функция f(x) стремится
к тому же пределу, т.е. если
еорема
4. Пусть
даны три функции f(x),
u(x) и v(x),
удовлетворяющие неравенствам u(x)≤f(x)≤
v(x).
Если функции u(x) и v(x) имеют
один и тот же предел при x→a (или x→∞),
то и функция f(x) стремится
к тому же пределу, т.е. если
![]() ,
то
,
то ![]() .
.
Смысл этой теоремы понятен из рисунка.
Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.
Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.
Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.
Теорема
6. Если
две функции f(x) и g(x) при
всех значениях аргумента x удовлетворяют
неравенству f(x)≥
g(x) и
имеют пределы ![]() ,
то имеет место неравенство b≥c.
,
то имеет место неравенство b≥c.
Доказательство. По
условию теоремы f(x)-g(x)
≥0,
следовательно, по теореме 5 ![]() ,
или
,
или ![]() .
.
Билет 31.
![]()
Доказательство

Рассмотрим односторонние
пределы ![]() и
и ![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть ![]() .
Отложим этот угол на единичной окружности
(R =
1).
.
Отложим этот угол на единичной окружности
(R =
1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). ТочкаH — проекция точки K на ось OX.
Очевидно, что:
![]() (1)
(1)
(где SsectOKA — площадь сектора OKA)
![]()
![]()
![]()
(из ![]() : | LA |
= tgx)
: | LA |
= tgx)
Подставляя в (1), получим:
![]()
Так
как при ![]() :
:
![]()
Умножаем на sinx:
![]()
Перейдём к пределу:
![]()
![]()
![]()
Н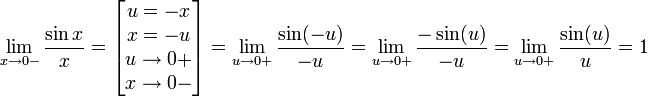 айдём
левый односторонний предел:
айдём
левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
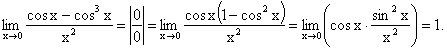



Билет 32 .

