Способы определения

Число e может быть определено несколькими способами.

• Через предел:

 (второй замечательный предел).

• Как сумма ряда:

 или  .

• Как единственное число a, для которого выполняется

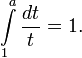
• Как единственное положительное число a, для которого верно

[Править]Свойства

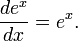• Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения 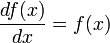 является функция 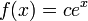 , где c — произвольная константа.

• Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.

• Число e является вычислимым (а значит, и арифметическим) числом.

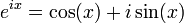• , см. формула Эйлера, в частности

  • 

• Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса»

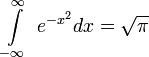
• Для любого комплексного числа z верны следующие равенства:

• Число e разлагается в бесконечную цепную дробь следующим образом:

, то есть

• 

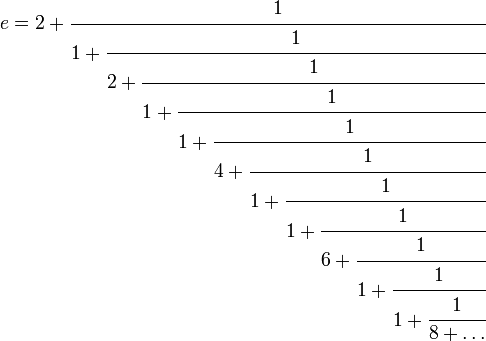
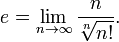
• Представление Каталана:

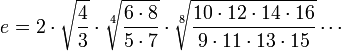
Билет 27.

Теорема о вложенных отрезках

 Пусть дана последовательность отрезков [а₁;b₁], [а₂;b₂],…, [а_n;b_n],… таких, что каждый последующий содержится в предыдущем: [а₁; b₁]   [а₂; b₂]  …  [а_n; b_n]   …, т.е. a_n≤ a_n+1 < b_n+1≤ b_n для всех n и пусть   Будем называть эту последовательность последовательностью вложенных отрезков.   Теорема3. Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем отрезкам этой последовательности.  Д о к а з а т е л ь с т в о. Из условия теоремы следует, что левые концы отрезков образуют неубывающую последовательность а₁ ≤ a₂ ≤ a₃ ≤…≤ a_n≤…, а правые концы – невозрастающую последовательность b₁ ≥ b₂ ≥ b₃ ≥…≥ b_n ≥…. При этом последовательность левых концов ограничена сверху, а последовательность правых концов ограничена снизу, так как a_n≤ b₁, а b_n≥ a₁ для любого n. Следовательно, на основе теоремы Больцано – Вейерштрасса эти последовательности имеют предел.  Пусть  , а  . Тогда из условия   следует, что c ' = c '', т.е. последовательности {a_n} и {b_n} имеют общий предел. Обозначая этот предел буквой с, получаем, что для любого номера n справедливы неравенства a_n≤ c ≤ b_n, т.е. точка с принадлежит всем отрезкам последовательности вложенных отрезков.  Докажем теперь, что такая точка только одна. Допустим, что существует еще одна точка c₁ (c₁ ≠ c), принадлежащая всем отрезкам последовательности вложенных отрезков. Тогда для любого n > N должно выполнятся неравенство  , и, следовательно, начиная с некоторого номера, b_n - a_n ≥ | c₁ - c |, что противоречит условию теоремы.

Билет 28.

Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры.

Понятие функции одной переменной  Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу  . Если величина сохраняет постоянное значение лишь в условиях данного процесса, она называется параметром. Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении:   , где   - путь,  - время,   - параметр. Определение. Если каждому элементу   множества   ставится в соответствие вполне определенный элемент  множества  , то тогда говорят, что на множестве  задана функция . При этом   называется независимой переменной  (или аргументом),   - зависимой переменной, а буква  обозначает закон соответствия. Множество   называется областью определения (или существования) функции, а множество   - областью значений функции. Если множество   специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной  , т.е. множество таких значений  , при которых функция   вообще имеет смысл. Способы задания функций: а) Аналитический способ, если функция задана формулой вида  . Этот способ наиболее часто встречается на практике. Например, функция   задана аналитически. Не следует, однако, смешивать функцию с ее аналитическим выражением. Так, например, одна функция   имеет два аналитических выражения:   (при  ) и  (при  ). б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента   и соответствующие значения функции  , например, таблица логарифмов,  гармонические функции и т.д. ,  ,  . в) Графический способ состоит в изображении графика функции - множества точек   плоскости, абсциссы которых есть значения аргумента  , а ординаты – соответствующие им значения функции  . г) Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле:  , если  - иррационально. Основные свойства функций 1) Четность и нечетность. Функция   называется четной, если для любых значений   из области определения   и нечетной, если . В противном случае функция   называется функцией общего вида. Пример. а) Функция   - четная (рис.3.3 а). т.к  ; б) Функция  - нечетная (рис.3.3 б).  ; в) Функция   - общего вида (рис.3.3 в).  . График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. 2) Монотонность. Функция   называется возрастающей (убывающей) на промежутке  , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями. Пример. 1) Функция   -  на интервале    монотонно возрастает (рис.3.4а).  2) Функция   - на интервале    монотонно убывает (рис.3.4 б). 3) Ограниченность. Функция   называется ограниченной на промежутке  , если существует такое положительное число  , что   для любого  . В противном случает функция называется неограниченной. - ограничена на всей числовой оси, т.к.   для любого  . 4) Периодичность. Функция   называется периодической с периодом  , если для любых   из области определения функции  . Пример. , период  , т.к. для любых    .

Билет 29.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально, под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а, также, описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).

Предел фу́нкции — одно из основных понятий математического анализа.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).