Расстояние от точки до прямой

Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

            Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:

                                                                                                (1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.

            Если преобразовать первое уравнение системы к виду:

A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

.

Есть система Ax + By + C=0, (1) A(y-y0) - B(x-x0)=0.(2) В первом уравнении прибавим и вычтем Ax0 и Bx0: A(x-x0) + B(y-y0) + Ax0 + By0 + C=0 (3) Выразим из второго ур-ния y-y0: y-y0 =(x-x0) * B / A  Подставим в третье: A(x-x0) + B^2 * (x-x0) / A + Ax0 + By0 + C=0 Сгруппируем x-x0: (x-x0)* (A^2 + B^2) / A + Ax0 + By0 + C=0 Отсюда выражаете x-x0. Для y-y0 аналогично.

Билет 13.

   Взаимное расположение двух прямых 

     Если прямые заданы уравнениями   и   то они:

     1) параллельны (но не совпадают) 

     2) совпадают 

     3) пересекаются 

     4) скрещиваются 

     Если   то случаи 1 - 4 имеют место, когда (  - знак отрицания условия):

     1)    

     2)    

     3)    

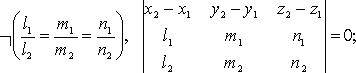
     4)    

     Расстояние между двумя параллельными прямыми 

     В координатах

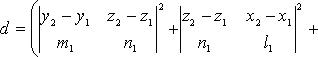
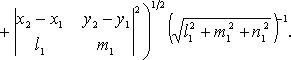
Угол между прямыми на плоскости

            Определение. Если заданы две прямые y = k₁x + b₁,  y = k₂x + b₂, то острый угол между этими прямыми будет определяться как

.

Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/k₂.

            Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = А,  В₁ = В. Если еще и С₁ = С, то прямые совпадают.

            Координаты точки пересечения двух прямых находятся как решение системы  уравнений этих прямых.

Билет 14.

СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ

Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:

1. тремя точками, не лежащими на одной прямой линии (рис.41);

а) модель		б) эпюр
Рисунок 41. Плоскость, заданная тремя точками, не лежащими на одной прямой

2. прямой линией и точкой, не принадлежащей этой прямой (рис.42);

а) модель		б) эпюр
Рисунок 42. Плоскость, заданная прямой линией и точкой, не принадлежащей этой линии

3. двумя пересекающимися прямыми (рис.43);

а) модель		б) эпюр
Рисунок 43. Плоскость, заданная двумя пересекающимися прямыми

4. двумя параллельными прямыми (рис.44);

а) модель		б) эпюр
Рисунок 44. Плоскость, заданная двумя параллельными прямыми

5. О положении плоскости относительно плоскостей проекций  удобно судить по её следам (рис.45).

Следом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная  плоскость  различают горизонтальный_П1, фронтальный _П2 и профильный _П3 следы.

а) модель		б) эпюр
Рисунок 45. Плоскость, заданная следами

Следы плоскости общего положения пересекаются  попарно на осях в точках _x,_y,_z. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.

Билет 15 .