Матан.

1 билет.

Сложение матриц Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен c_ij = a_ij + b_ij

Умножение матрицы на число Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен: b_ij = λa_ij

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца(Кольцо — это множество R, на котором заданы две бинарные операции: + и × )или поля (например, целых или комплексных чисел), которая представляет собой совокупность и , на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матричные операции

• Сложение и вычитание допускается только для матриц одинакового размера.

• Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть: A + Θ = A

• Все элементы нулевой матрицы равны нулю.

• Возводить в степень можно только квадратные матрицы.

• Ассоциативность сложения: A + (B + C) = (A + B) + C.

• Коммутативность сложения: A + B = B + A.

• Ассоциативность умножения: A(BC) = (AB)C.

• Вообще говоря, умножение матриц некоммутативно: . Используя это свойство, вводят коммутатор матриц.

• Дистрибутивность умножения относительно сложения:

A(B+C)=AB+AC; (B + C)A = BA + CA.

• С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.

• Свойства операции транспонирования матриц:

(A^T)^T =A (AB)^T =B^TA^T (A ⁻¹)^T =(A^T) ⁻¹,еслиОбратнаяМатрица(A-1)существует. (A+B)^T =A^T +B^T detA = detA^T

2 Билет.

Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность mxn , B — nxk , то размерность их произведения AB = C есть mxk.

Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.

Определение

Квадратная матрицаE_n = (e_ij) размера (порядка n), где e_ii = 1 для всякого  , и e_ij = 0 для всяких  , назвается единичной матрицей порядка n.

Единичную матрицу можно определить как матрицу (e_ij), у которой e_ij = δ_ij, где δ_ij - символ Кронекера.

Единичная матрица является частным случаем скалярной матрицы.

[править]Обозначение

Единичная матрица размера   обычно обозначается E_n и имеет вид:

Так же используется и другое обозначение: I_n.

Если из контекста ясно, какого размера матрица, то нижний индекс (указывающий порядок) опускается: E, I.

Свойства

• Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице:

AE = EA = A

• Квадратная матрица в нулевой степени дает единичную матрицу того же размера:

A⁰ = E

• При умножении матрицы на обратную ей тоже получается единичная матрица:

• Единичная матрица получается при умножении ортогональной матрицы на ей транспонированную:

AA^T = E

• Определитель единичной матрицы равен единице:

.

3 Билет.

Определитель - число, характеризующее матрицу. Определителем матрицы 1-го порядка А=(а₁₁)  является единственный элемент этой матрицы. Определителем 2-го порядка называется число, характеризующее матрицу 2-го порядка, которое находится по следующему правилу: из произведений элементов главной диагонали вычитается произведение элементов второй диагонали матрицы А. Определителем матрицы 3-го порядка называется число, вычисляемое по правилу Сарруса. Правило Сарруса:  определитель 3-го порядка  равен алгебраической сумме 6-ти тройных произведений элементов, стоящих в разных строках и разных столбцах; со знаком «+» берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников, чьи основания параллельны главной диагонали, остальные слагаемые берутся со знаком «-». . Свойства определителей. Если к.-л. строка или столбец в матрице состоит из одних нолей, то det этой матрицы равен 0. 2) При транспонировании матрицы её определитель не изменяется. 3) Если все элементы к.-л. строки или столбца матрицы умножить на одно и то же число, то и det этой матрицы умножится на это же число. 4) При перестановке местами 2-х строк или столбцов матрицы её определитель меняет свой знак на противоположный. 5) Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0. 6)Если 2 строки или 2 столбца матрицы пропорциональны, то её det равен 0. 7) Сумма произведений элементов к.-л. строки или столбца матрицы и другой строки или столбца равна 0. 8) Определитель матрицы не изменяется если к элементам одной строки или столбца прибавить элементы другой строки или столбца, умноженный на одно и то же число. 9)Если к.-л. столбец или строка матрицы представляет собой сумму 2-х элементов, то det этой матрицы может быть представлен в виде суммы   2-х определителей.

Разложить определитель можно по любой строке или столбцу, то при разложении по полученной в результате линейной комбинации строке, определитель равен произведению ненулевого элемента этой строки на его алгебраическое дополнение (взятое с соответствующим знаком).

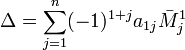
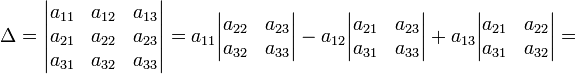
= a₁₁a₂₂a₃₃ − a₁₁a₂₃a₃₂ − a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ − a₁₃a₂₂a₃₁

Свойства

• Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице:

AE = EA = A

• Квадратная матрица в нулевой степени дает единичную матрицу того же размера:

A⁰ = E

• При умножении матрицы на обратную ей тоже получается единичная матрица:

• Единичная матрица получается при умножении ортогональной матрицы на ей транспонированную:

AA^T = E

• Определитель единичной матрицы равен единице:

.

Билет 4

Обратная матрица Обра́тная ма́трица — такая матрица A-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:AA^-1 =A^-1A=E Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

C * (союзная, взаимная, присоединённая) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.

Алгебраическим дополнением элемента aij матрицы A называется число Aij = ( − 1)^{i + j}M_ij, где M_ij — дополнительный минор, определитель матрицы, получающейся из исходной матрицы A путем вычёркивания i -й строки и j -го столбца.

Билет 5

Ранг матрицы Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы. Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

• прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу  ,   и прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение   указывает на то, что матрица   может быть получена из   путём элементарных преобразований (или наоборот).

Матрица   имеет ступенчатый вид, если:

1. Все нулевые строки матрицы   стоят последними;

2. Для любой ненулевой строки матрицы   (пусть для определённости её номер равен  ) справедливо следующее: если 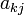  — первый ненулевой элемент строки  , то  .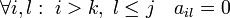

Билет 6.

1. Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].