- •Понятие матрицы. Осн. Операции над матрицами. Сложение матриц и умножение матрицы на число. Св-ва этих операций.
- •Понятие матрицы. Осн. Операции над матрицами. Умножение матриц и транспонирование матриц. Св-ва этих операций.
- •Определители 2-ого и 3-его порядков. Понятие определителя n-порядка.
- •Миноры и алгебраические дополнения эл-тов матрицы. Способы вычисления определителей.
- •Обратная матрица.
- •Ранг матрицы. Способы вычисления. Теорема о ранге матрицы. Метод окаймляющих миноров.
- •8. Ранг матрицы. Способы вычисления. Метод элементарных преобразований.
- •9. Понятие слау. Осн. Опред-я. Матричная запись слау.
- •10. Совместность слау. Теорема Кронекера-Капелли.
- •11. Формулы Крамера. Решение системы с использованием обратной матрицы.
- •12. Структура общего решения совместной неоднородной слау.
- •13. Однородные слау. Св-ва решений. Фундаментальная система решений однородной слау.
- •14. Метод последовательных исключений Гаусса решения слау.
- •15. Декартовы прямоугольные системы координат. Полярные системы координат.
- •16. Простейшие задачи аналитической геометрии.
- •17. Понятие вектора. Линейные операции над в-ми и их св-ва.
- •18. Коллинеарность в-ов. Геом. Смысл линейной зависимости двух в-ов.
- •19. Компланарность. Геом. Смысл линейной зависимости 3-ёх в-ов.
- •20 Линейная зависимость четырех векторов.
- •21. Базис и координаты в-ов на пл-ти и в пространстве. Декартовы прямоугольные координаты, основные формулы. Геом. Смысл декартовых прямоугольных координат вектора.
- •Базис в декартовой прямоугольной системе координат. Геометрический смысл декартовых прямоугольных координат вектора.
- •22. Скалярное произведение в-ов. Опред., осн. Св-ва. Выражение скалярного произведения через координаты сомножителей.
- •23. Векторное произведение. Опред., геом. Смысл, осн. Св-ва. Выражение векторного произведения через координаты сомножителей.
- •24. Смешанное произв. В-ов, его геом. Смысл и осн. Св-ва. Выражение смешанного произведения в-ов через координаты сомножителей.
- •25. Общее ур-ие прямой на плоскости и его исследование. Ур-ие прямой в отрезках.
- •Уравнение прямой в пространстве, проходящей через 2 заданные точки.
- •26. Каноническое ур-ие прямой на плоскости. Ур-ие прямой, проходящей через две заданные точки. Параметрические ур-ия прямой. Ур-ие прямой с угловым коэффициентом.
- •27. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
- •28. Нормированное ур-ие прямой на пл-ти. Приведение общего ур-ия прямой на пл-ти к нормированному виду. Расстояние от точки до прямой на пл-ти.
- •30. Угол между 2-мя пл-ми. Условия || и двух плоскостей. Ур-ие пл-ти, проходящей через три заданные точки.
- •31. Нормированное ур-ие пл-ти. Приведение общего ур-ия пл-ти к нормированному виду. Расстояние от точки до пл-ти.
- •32. Прямая в пространстве как линия пересечения двух пл-тей. Канонические и параметрические ур-ия. Ур-ия прямой, проходящей через две заданные точки.
- •33. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых. Исследование взаимного расположения двух прямых в пространстве.
- •Преобразование матрицы линейного оператора при переходе к новому базису.
20 Линейная зависимость четырех векторов.
Теорема: Любые четыре вектора линейно зависимы.
Док-во: Пусть среди четырех векторов а, b, с и d никакая тройка векторов не компланарна, в противном случае все четыре вектора линейно зависимы.
Приведем все четыре вектора а, b, с и d к общему началу О и проведем через конец D вектора d плоскости, параллельные плоскостям, определяемым парами векторов be, ас и ab (т.к. векторы некомпланарны, значит, они определяют некоторую плоскость).
Точки пересечения указанных плоскостей с прямыми, на которых лежат векторы a, b и с, обозначим соответственно А, В и С.
Из параллелограмма OCDE по правилу параллелограмма сложения векторов вытекает, что d = ОС + ОЕ, а из параллелограмма ОВЕА— что OE=OA+OB. То есть d = OA + OB+ OC
Т.к. вектор ОА коллинеарен ненулевому вектору а, следовательно, найдется вещественное число λ такое, что
0A = λ *а.
Аналогично
OB = μ*b, OC = η*c .
Подставив , получим d = λ *a + μ *b + η*c или λ *a + μ*b+ η*c+(-l)d = 0.
Так как из четырех чисел λ, μ, η, -1 одно заведомо отлично от нуля, то последнее равенство доказывает линейную зависимость векторов а, b, с и d.
Следствие. Каковы бы ни были некомпланарные векторы а, b и с, для любого вектора d найдутся такие вещественные числа λ, μ, η, что
d= λ *а + μ*b+ η*c.
21. Базис и координаты в-ов на пл-ти и в пространстве. Декартовы прямоугольные координаты, основные формулы. Геом. Смысл декартовых прямоугольных координат вектора.
Опред.: 3 ЛНЗ в-ра a, b, c образуют базис в пространстве.
Опред.: 2 ЛНЗ вектора a, b, лежащие в пл-ти , образуют базис в этой пл-ти.
Утв.: Любая тройка некомпланарных векторов образует базис в пространстве.
Утв.: Любая пара неколлинеарных векторов образует базис в плоскости, образованной этими векторами.
Пусть a, b, c - некоторый базис пространства d = αa+βb+Ϫc – разложение d по базису a, b, c.
, , - координаты d в базисе a, b, c. d = {λ,μ,η}
Аффинные координаты (АК) образуются заданием базиса a, b, c и началом координат.
Аффинные
координаты т.M
равны координатам
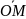 в базисе a,
b,
c.
в базисе a,
b,
c.
Частным случаем аффинной системы координат является декартова прямоугольная система координат (ДПСК).
a,
b,
c
I,
j,
k
, |i|
= |j|
= |k|
= 1, I ,
j
k,
I
k
- взаимно ортогональные.
,
j
k,
I
k
- взаимно ортогональные.
Любой вектор d может быть единственным образом представлен в виде линейной комбинации векторов I, j, k, т.е. этот вектор имеет единственным образом определенные координаты в базисе I, j, k.
, , x, y, z
d
= xi
+ yj
+ zk,
d
= {x,
y,
z},
где x,
y,
z
– координаты
 .
.
Д.П.Координаты
точки M
равны координатам
 в базисе
в базисе
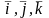 .
.
Базис в декартовой прямоугольной системе координат. Геометрический смысл декартовых прямоугольных координат вектора.
Любой
вектор
![]() может быть единственным образом
представлен в виде линейной комбинации
векторов
,
т.е. этот вектор имеет единственным
образом определенные координаты в
базисе
может быть единственным образом
представлен в виде линейной комбинации
векторов
,
т.е. этот вектор имеет единственным
образом определенные координаты в
базисе
![]() .
.
 ,
,
 ,
где x,
y,
z
– координаты
.
,
где x,
y,
z
– координаты
.
Д.П.Координаты точки M равны координатам в базисе .
Геометрический смысл ДПК вектора.
Теорема:
ДПК
вектора
равны проекциям этого вектора на
координатные оси
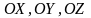 соответственно.
соответственно.
Док-во:

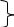
 ||
||
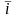
x:
= x
x:
= x
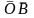 ||
||
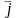
y:
= y
( * )
y:
= y
( * )
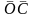 ||
||
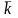
z:
= z
z:
= z
Нам
надо показать, что
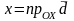 ,
,
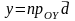 ,
,
 Т.к. параллелепипед прямоугольный
Т.к. параллелепипед прямоугольный
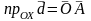 ,
,
 ,
,

требуется доказать, что x = , y = , z = .
Из
( * ) :
 ,
,
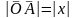
З наки:
1) Если
и
одинаково направлены
OA
> 0 OA
и x
имеют
наки:
1) Если
и
одинаково направлены
OA
> 0 OA
и x
имеют
Из ( * ) x > 0 одинаковые знаки
2) Если и противоположно направлены OA < 0, ( * ) : x < 0 OA и x – имеют одинаковые знаки x = OA . Аналогично, y = OB , z = OC.