
- •Понятие матрицы. Осн. Операции над матрицами. Сложение матриц и умножение матрицы на число. Св-ва этих операций.
- •Понятие матрицы. Осн. Операции над матрицами. Умножение матриц и транспонирование матриц. Св-ва этих операций.
- •Определители 2-ого и 3-его порядков. Понятие определителя n-порядка.
- •Миноры и алгебраические дополнения эл-тов матрицы. Способы вычисления определителей.
- •Обратная матрица.
- •Ранг матрицы. Способы вычисления. Теорема о ранге матрицы. Метод окаймляющих миноров.
- •8. Ранг матрицы. Способы вычисления. Метод элементарных преобразований.
- •9. Понятие слау. Осн. Опред-я. Матричная запись слау.
- •10. Совместность слау. Теорема Кронекера-Капелли.
- •11. Формулы Крамера. Решение системы с использованием обратной матрицы.
- •12. Структура общего решения совместной неоднородной слау.
- •13. Однородные слау. Св-ва решений. Фундаментальная система решений однородной слау.
- •14. Метод последовательных исключений Гаусса решения слау.
- •15. Декартовы прямоугольные системы координат. Полярные системы координат.
- •16. Простейшие задачи аналитической геометрии.
- •17. Понятие вектора. Линейные операции над в-ми и их св-ва.
- •18. Коллинеарность в-ов. Геом. Смысл линейной зависимости двух в-ов.
- •19. Компланарность. Геом. Смысл линейной зависимости 3-ёх в-ов.
- •20 Линейная зависимость четырех векторов.
- •21. Базис и координаты в-ов на пл-ти и в пространстве. Декартовы прямоугольные координаты, основные формулы. Геом. Смысл декартовых прямоугольных координат вектора.
- •Базис в декартовой прямоугольной системе координат. Геометрический смысл декартовых прямоугольных координат вектора.
- •22. Скалярное произведение в-ов. Опред., осн. Св-ва. Выражение скалярного произведения через координаты сомножителей.
- •23. Векторное произведение. Опред., геом. Смысл, осн. Св-ва. Выражение векторного произведения через координаты сомножителей.
- •24. Смешанное произв. В-ов, его геом. Смысл и осн. Св-ва. Выражение смешанного произведения в-ов через координаты сомножителей.
- •25. Общее ур-ие прямой на плоскости и его исследование. Ур-ие прямой в отрезках.
- •Уравнение прямой в пространстве, проходящей через 2 заданные точки.
- •26. Каноническое ур-ие прямой на плоскости. Ур-ие прямой, проходящей через две заданные точки. Параметрические ур-ия прямой. Ур-ие прямой с угловым коэффициентом.
- •27. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
- •28. Нормированное ур-ие прямой на пл-ти. Приведение общего ур-ия прямой на пл-ти к нормированному виду. Расстояние от точки до прямой на пл-ти.
- •30. Угол между 2-мя пл-ми. Условия || и двух плоскостей. Ур-ие пл-ти, проходящей через три заданные точки.
- •31. Нормированное ур-ие пл-ти. Приведение общего ур-ия пл-ти к нормированному виду. Расстояние от точки до пл-ти.
- •32. Прямая в пространстве как линия пересечения двух пл-тей. Канонические и параметрические ур-ия. Ур-ия прямой, проходящей через две заданные точки.
- •33. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых. Исследование взаимного расположения двух прямых в пространстве.
- •Преобразование матрицы линейного оператора при переходе к новому базису.
Уравнение прямой в пространстве, проходящей через 2 заданные точки.
Прямую
линию в пространстве можно задавать
как линию пересечения двух различных
и не параллельных плоскостей: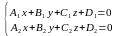 .
Любой ненулевой вектор, параллельный
данной прямой называется направляющим
вектором этой прямой. Найдём уравнение
прямой, проходящей через данную точку
M1(x1,y1,z1),
и имеющей заданный направляющий вектор
q={l,m,n}.
Очевидно, точка M(x,y,z)
лежит на указанной прямой тогда и только
тогда, когда вектор
.
Любой ненулевой вектор, параллельный
данной прямой называется направляющим
вектором этой прямой. Найдём уравнение
прямой, проходящей через данную точку
M1(x1,y1,z1),
и имеющей заданный направляющий вектор
q={l,m,n}.
Очевидно, точка M(x,y,z)
лежит на указанной прямой тогда и только
тогда, когда вектор
 и
q={l,m,n}
коллинеарны, т.е. тогда и только тогда,
когда координаты этих векторов
пропорциональны:
и
q={l,m,n}
коллинеарны, т.е. тогда и только тогда,
когда координаты этих векторов
пропорциональны:
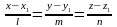 (1).
Это и есть искомое уравнение прямой,
называемое каноническим уравнением
прямой. Запишем уравнение прямой,
проходящей через две данные отличные
друг от друга точки M1(x1,y1,z1)
и M2(x2,y2,z2).
За направляющий вектор
(1).
Это и есть искомое уравнение прямой,
называемое каноническим уравнением
прямой. Запишем уравнение прямой,
проходящей через две данные отличные
друг от друга точки M1(x1,y1,z1)
и M2(x2,y2,z2).
За направляющий вектор
 и, учитывая, что прямая проходит через
точку M1(x1,y1,z1),
из канонического уравнения (1) получим
уравнение искомой прямой в виде
и, учитывая, что прямая проходит через
точку M1(x1,y1,z1),
из канонического уравнения (1) получим
уравнение искомой прямой в виде
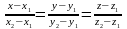 .
Примем за параметр t=
,
т.е.
.
Примем за параметр t=
,
т.е.
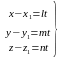 ,
следовательно,
,
следовательно,
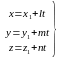 .
Это уравнение называется параметрическим
уравнением прямой.
.
Это уравнение называется параметрическим
уравнением прямой.
уравнение прямой в отрезках на плоскости. Параметрические уравнения прямой
Пусть уравнение Ах+Ву+С=0 – полное.
Ах+Ву= -С/-С
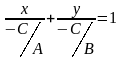
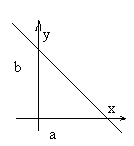 ,
-С/А=а, -С/В=b,
тогда получим
,
-С/А=а, -С/В=b,
тогда получим
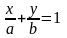 - уравнение прямой в отрезках , где a
u
b-величины
отрезков, которые прямая отсекает на
осях координат.
- уравнение прямой в отрезках , где a
u
b-величины
отрезков, которые прямая отсекает на
осях координат.

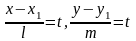
 параметрическое
уравнение прямой.
параметрическое
уравнение прямой.
26. Каноническое ур-ие прямой на плоскости. Ур-ие прямой, проходящей через две заданные точки. Параметрические ур-ия прямой. Ур-ие прямой с угловым коэффициентом.
Любой ненулевой вектор || данной прямой наз-ся направляющим вектором этой прямой.

 q={l,m},
М(х,у)L
тогда и только тогда, когда
q={l,m},
М(х,у)L
тогда и только тогда, когда
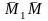 ||
|| ,
где |М1М|={x-x1,y-y1}
,
где |М1М|={x-x1,y-y1}
 -каноническое
уравнение прямой
-каноническое
уравнение прямой q=M1M2={x2-x1,y2-y1},
x2-x1=l,
y2-y1=m
q=M1M2={x2-x1,y2-y1},
x2-x1=l,
y2-y1=m
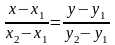 -
уравнение прямой на, проходящей через
две заданные точки.
-
уравнение прямой на, проходящей через
две заданные точки.
Параметрические уравнения прямой
Пусть уравнение Ах+Ву+С=0 – полное. Ах+Ву= -С ⇒ , обозначим -С/А=а, -С/В=b, тогда получим - уравнение прямой в отрезках , где a и b-величины отрезков, которые прямая отсекает на осях координат. ⇒ ⇒ —параметрическое уравнение прямой.
Уравнение прямой с угловым коэффициентом.
= NAM — угол наклона прямой L к оси ОХ. tg=k наз-ся угловым коэффициентом этой прямой.
Теорема:
Если
прямая непараллельна оси ОУ и имеет
направляющий вектор
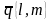 ,
то
,
то
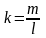
Док-во:
=(L,
OX),
= ( )
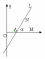
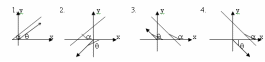
рис.1,3: =
tg
= tg
l=
|q|
cos,
m=|q|
cos
(\2-)=sin
)
рис.1,3: =
tg
= tg
l=
|q|
cos,
m=|q|
cos
(\2-)=sin
 рис 2,4: ≠,
=
– ,
тогда tg
= tg(
- )
= – tg
l
= |q|cos
Получим в общем случае: m=|q|
cos
(3\2-)
= – |q|sin
рис 2,4: ≠,
=
– ,
тогда tg
= tg(
- )
= – tg
l
= |q|cos
Получим в общем случае: m=|q|
cos
(3\2-)
= – |q|sin
27. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
Пусть имеются прямая L1:A1x+B1y+C1=0 и L2:A2x+B2y+C2=0. n1={A1,B1}, n2={A2,B2}.
 ,
cos=
,
cos= L1||L2n1||n2
L1||L2n1||n2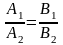
L1L2n1n2A1A2+B1B2=0
Если прямые заданы своими каноническими уравнениями, то

(L1,L2)=(q1,q2),
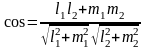 ,
L1||L2q1||q2
,
L1||L2q1||q2
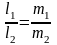
L1L2q1q2l1l2+m1m2=0
Прямые L1 и L2 параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, т. е. существует такое число , что: А1=А, В1=В.
Прямые L1 и L2 перпендикулярны, когда скалярное произведение их нормальных векторов равно 0.
