5. Миноры и алгебраические дополнения эл-тов матрицы. Способы вычисления определителей.

Минором данного эл-та определителя n-порядка, назыв. определитель

(n-1)-порядка, полученный вычёркиванием i-строки и j-столбца, на пересечении которых стоит данный элемент. Алгебр. дополнением данного эл-та определителя n-порядка, назыв. минор этого эл-та, взятый со знаком «+»/«-», в зависимости от того, чётна или нечётна сумма номеров строки и столбца, на пересечении которых стоит данный эл-т.

Способы вычисления определителей:

Теорема: (разложение определителя по i-строке) Опред-ль равен сумме произведений всех эл-ов какой-либо строки на их алгебр. дополнение.

Аналогичное разложение можно получить и для любого столбца опред-ля.

Св-во 9 позволяет так преобразовать опред-ль, чтобы в некоторой строке все эл-ты были заменены нулями кроме одного.

6. Обратная матрица.

Опред.: если существуют квадратные матрицы B и А одного порядка, удовлетворяющие условию: BA = AB = E, где Е — единичная матрица того же самого порядка, что и матрица А, то матрица B назыв. обратной к матрице А и обозначается А^-1.

Каждая кв. матрица с опред-ем, не равным нулю имеет обратную матрицу и притом только одну.

Вычисление обр. матрицы:

Рассм. квадратную матрицу 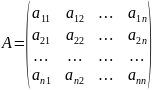. Обозначим .

Кв. матрица А называется невырожденной, или неособенной, если ее опред-ль отличен от 0, и вырожденной, или особенной, если .

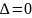Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее опред-ль был отличен от 0.

Матрица, обратная матрице А, обозначается через , так что . Обратная матрица вычисляется по формуле

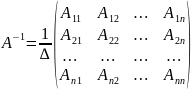, где — алгебраические дополнения эл-в .

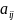Для нахождения обратных матриц больших порядков, обычно применяют следующую формулу 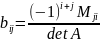, где — дополнительный минор элемента 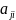матрицы А.

7. Ранг матрицы. Способы вычисления. Теорема о ранге матрицы. Метод окаймляющих миноров.

Опред.: Максимальное число линейно независимых в-ов системы, назыв. рангом этой матрицы.

Т.к. столбцы произв. матрицы – это m-мерные в-ра, то ранг системы столбцов, т.е. максимальное число ЛНЗ столбцов матрицы, назыв. рангом этой матрицы.

Строки – тоже в-ры. Можно показать, что ранг системы = рангу системы столбцов, т.е. = рангу этой матрицы.

Способы вычисл.: 1. Метод окаймляющих миноров. A(m ˟ n). Нас будут интересовать порядки тех миноров, которые отличны от 0, наивысшие из этих порядков. Если все миноры порядка К матрицы = 0, то и равны 0 и все миноры более высоких порядков.

Теорема: Наивысший порядок отличный от 0 миноров матрицы равен рангу этой матрицы. (теорема о ранге)

Правило вычисл. ранга матрицы: При вычисл. ранга матрицы, следует переходить от миноров меньших порядков к минорам высших. Если уже найден минор r-порядка ≠ 0, то требуют вычисления лишь миноры (r+1)-порядка, окаймляющий найденный минор. Если все они = 0, то ранг матрицы = r.

Следств.: Опред-ль n-порядка = 0 <=> когда между его строками существует линейная зависимость.

8. Ранг матрицы. Способы вычисления. Метод элементарных преобразований.

Опред.: Максимальное число линейно независимых в-ов системы, назыв. рангом этой матрицы.

Т.к. столбцы произв. матрицы – это m-мерные в-ра, то ранг системы столбцов, т.е. максимальное число ЛНЗ столбцов матрицы, назыв. рангом этой матрицы.

Строки – тоже в-ры. Можно показать, что ранг системы = рангу системы столбцов, т.е. = рангу этой матрицы.

Правило вычисл. ранга матрицы: При вычисл. ранга матрицы, следует переходить от миноров меньших порядков к минорам высших. Если уже найден минор r-порядка ≠ 0, то требуют вычисления лишь миноры (r+1)-порядка, окаймляющий найденный минор. Если все они = 0, то ранг матрицы = r.

Следств.: Опред-ль n-порядка = 0 <=> когда между его строками существует линейная зависимость.

Метод элементарных преобразований.

Опред.: Эл. Преобразованиями матрицы назыв. след. преобразования: 1. Перемена мест любых двух строк или столбцов; 2. Умножение любой строки или столбца на произвольные ≠ 0 числа; 3. Прибавление к любой строке или столбцу любую другую строку или столбец.

Теорема: эл. преобразования не меняют ранг матрицы, т.е. эл. преоб. Не влияют на ЛЗ или ЛНЗ системы. Поэтому, перед вычислением ранга следует при каждом эл. преоб-нии, привести матрицу к наиболее простому виду.

Опред.: Матрица (m ˟ n) имеет диагональную форму, если все её эл-ты равны 0, кроме 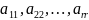, равных единице. Очевидно ранг матрицы = r.

Утв.: Любую матрицу можно эл. преобр-ями привести к диагональной форме.

Т.о., при вычислении ранга матрицы следует привести эту матрицу эл. преобр-ми к диагональной форме и подсчитать число единиц, стоящих в последней главной диагонали.