
- •Понятие матрицы. Осн. Операции над матрицами. Сложение матриц и умножение матрицы на число. Св-ва этих операций.
- •Понятие матрицы. Осн. Операции над матрицами. Умножение матриц и транспонирование матриц. Св-ва этих операций.
- •Определители 2-ого и 3-его порядков. Понятие определителя n-порядка.
- •Миноры и алгебраические дополнения эл-тов матрицы. Способы вычисления определителей.
- •Обратная матрица.
- •Ранг матрицы. Способы вычисления. Теорема о ранге матрицы. Метод окаймляющих миноров.
- •8. Ранг матрицы. Способы вычисления. Метод элементарных преобразований.
- •9. Понятие слау. Осн. Опред-я. Матричная запись слау.
- •10. Совместность слау. Теорема Кронекера-Капелли.
- •11. Формулы Крамера. Решение системы с использованием обратной матрицы.
- •12. Структура общего решения совместной неоднородной слау.
- •13. Однородные слау. Св-ва решений. Фундаментальная система решений однородной слау.
- •14. Метод последовательных исключений Гаусса решения слау.
- •15. Декартовы прямоугольные системы координат. Полярные системы координат.
- •16. Простейшие задачи аналитической геометрии.
- •17. Понятие вектора. Линейные операции над в-ми и их св-ва.
- •18. Коллинеарность в-ов. Геом. Смысл линейной зависимости двух в-ов.
- •19. Компланарность. Геом. Смысл линейной зависимости 3-ёх в-ов.
- •20 Линейная зависимость четырех векторов.
- •21. Базис и координаты в-ов на пл-ти и в пространстве. Декартовы прямоугольные координаты, основные формулы. Геом. Смысл декартовых прямоугольных координат вектора.
- •Базис в декартовой прямоугольной системе координат. Геометрический смысл декартовых прямоугольных координат вектора.
- •22. Скалярное произведение в-ов. Опред., осн. Св-ва. Выражение скалярного произведения через координаты сомножителей.
- •23. Векторное произведение. Опред., геом. Смысл, осн. Св-ва. Выражение векторного произведения через координаты сомножителей.
- •24. Смешанное произв. В-ов, его геом. Смысл и осн. Св-ва. Выражение смешанного произведения в-ов через координаты сомножителей.
- •25. Общее ур-ие прямой на плоскости и его исследование. Ур-ие прямой в отрезках.
- •Уравнение прямой в пространстве, проходящей через 2 заданные точки.
- •26. Каноническое ур-ие прямой на плоскости. Ур-ие прямой, проходящей через две заданные точки. Параметрические ур-ия прямой. Ур-ие прямой с угловым коэффициентом.
- •27. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
- •28. Нормированное ур-ие прямой на пл-ти. Приведение общего ур-ия прямой на пл-ти к нормированному виду. Расстояние от точки до прямой на пл-ти.
- •30. Угол между 2-мя пл-ми. Условия || и двух плоскостей. Ур-ие пл-ти, проходящей через три заданные точки.
- •31. Нормированное ур-ие пл-ти. Приведение общего ур-ия пл-ти к нормированному виду. Расстояние от точки до пл-ти.
- •32. Прямая в пространстве как линия пересечения двух пл-тей. Канонические и параметрические ур-ия. Ур-ия прямой, проходящей через две заданные точки.
- •33. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых. Исследование взаимного расположения двух прямых в пространстве.
- •Преобразование матрицы линейного оператора при переходе к новому базису.
28. Нормированное ур-ие прямой на пл-ти. Приведение общего ур-ия прямой на пл-ти к нормированному виду. Расстояние от точки до прямой на пл-ти.
Нормированное уравнение прямой на плоскости.
Если
уравнения заданы: L1:y=k1x+b1,
L2:y=k2x+b2
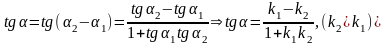 если к2>к1tg=
если к2>к1tg= ,
n
L,
n
L=P,
|OP|=P,
|n|=1
, nOP.
,
n
L,
n
L=P,
|OP|=P,
|n|=1
, nOP.
Если
т.Р= т.О(0,0)
n-произвольный.
= (n,OX),
n={|n|cos,|n|cos(/2-)}
n{cos,sin},т.М(x,y)-точка
L.
Очевидно, что М
L,
если пр n
M=
т.Р, т.е. пр n
OM
=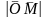 = -P,
= -P,
 ,OM={x,y},
,OM={x,y},
 .
xcos+ysin-p=0
-
нормированное
уравнение прямой
.
xcos+ysin-p=0
-
нормированное
уравнение прямой
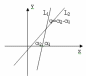
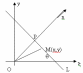
Приведение общего ур-ия прямой на пл-ти к нормированному виду.
Расстояние
от точки до прямой на плоскости есть
отклонение (M,L).
Отклонением (M,L)
называется число +d,
если точка М и точка О лежат по разные
стороны от прямой, и –d,
если по одну сторону. Для того чтобы
найти отклонение точки М0(x0,y0)
от прямой L
cледует
в левую часть нормированного уравнения
этой прямой вместо x
и y
подставить координаты (x0,y0)
точки М0.
Ax+By+C=0
Xcos+Ysin-p=0
(приведение к нормированному виду). Так
как эти два уравнения определяют одну
и ту же прямую
t: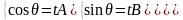
1=t2(A2+B2).
P=>0,
t
и c
имеют противоположные знаки
1=t2(A2+B2).
P=>0,
t
и c
имеют противоположные знаки
(M,L)= Xcos+Ysin-p.
Для того чтобы привести общее уравнение прямой к нормированному виду следует умножить это уравнение на нормирующий множитель t знфк которого противоположен знаку c.
Расстояние от точки до прямой
Теорема. Если
задана точка М(х0,
у0),
то расстояние до прямой Ах + Ву + С =0
определяется как![]()
Доказательство.
Пусть
точка М1(х1,
у1)
– основание перпендикуляра, опущенного
из точки М на заданную прямую. Тогда
расстояние между точками М и М1:
![]() (1)
(1)
Координаты
x1
и
у1
могут
быть найдены как решение системы
уравнений:
![]()
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x–x0)+B(y–y0)+Ax0+By0+ C=0, то, решая, получим:
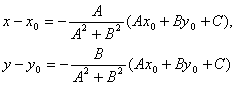 Подставляя
эти выражения в уравнение (1), находим:
Подставляя
эти выражения в уравнение (1), находим:
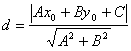 .
.
29. Пл-ть в трехмерном пространстве. Общее ур-ие пл-ти и его исследование. Ур-ие пл-ти в отрезках.
Общее уравнение плоскости и его исследование.
A x+By+Cz+D=0 (1) A, B, C, D – любые константы, требуется чтобы хотя бы один из коэффициентов был отличен от 0. Это есть общее уравнение плоскости. M0(x0,y0,z0) – коор. удовлетворяют (1). Ax0+By0+Cz0+D=0 (2). Если (1)-(2): A(x-x0)+B(y-y0)+C(z-z0)=0
M(x,y,z), n={A,B,C}, M0Mn=A(x-x0)+C(y-y0)+c(z-z0)=0, т.е. M0Mn=0 <=> M0M n, а т.к. M(x,y,z) это любая точка плоскости => n П, n={A,B,C}→ нормальный вектор плоскости.
Замечание: Пусть уравнение Ax+By+Cz+D=0 и A1x+B1y+C1z+D1=0, это есть уравнение одной и той же плоскости => существует число t: A1=tA; B1=tB; C1=tC; D1=tD
Док. n={A,B,C}; n1={A1,B1,C1} т.к. плоскость одна и та же => n1║n=> существует t: n1=tn=> A1=tA; B1=tB; C1=tC. Возьмем любую точку M0(x0,y0,z0) П
Ax0+By0+Cz0+D=0 уравнение умножим на t, A1x0+B1y0+C1z0+D1=0 ⇒ (A1-tA)x0+(B1-tB)y0+(C1-tC)z0+(D1-tD)=0 => равенство выполняется, если D1-tD=0 =>D1=tD. Общее уравнение плоскости (1) называется полным если все его коэффициенты отличны от 0, в противном случае уравнение называется не полным.
Ax+By+Cz+D=0
Все случаи неполных уравнений:
1) D=0 Ax+By+Cz=0→ проходит через начало коор.
2) A=0 By+Cz++D=0→ уравнение плоскости паралл. оси OX
3) B=0 Ax+Cz+D=0→ уравнение плоскости паралл. оси OY
4) C=0 Ax+By+D=0→ уравнение плоскости паралл. оси OZ
5) A=0 и B=0 Cz+D=0→ уравнение плоскости паралл. OXY
6) A=0 и C=0 By+D=0→ паралл. OXZ
7) B=0, C=0 Ax+D=0→ паралл. OYZ
8) A=0, B=0 и D=0 Cz=0→ OXY
9) A=0, C=0, D=0 By=0→ OXZ
10) B=0, C=0, D=0 Ax=0→OYZ.
Уравнение плоскости в отрезках.
Рассмотрим
полное уравнение плоскости Ax+By+Cz+D=0
(1). Так как все коэффициенты A,
B,
C
и D
отличны от нуля, следовательно, можно
переписать это уравнение таким образом:
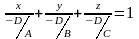 .
Обозначим
.
Обозначим
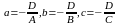 и приведём уравнение (1) к виду
и приведём уравнение (1) к виду
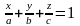 ,
называемому уравнением
плоскости в «отрезках».
Геометрический смысл чисел a,
b,
c
состоит в том,
,
называемому уравнением
плоскости в «отрезках».
Геометрический смысл чисел a,
b,
c
состоит в том,
что они равны величинам отрезков, которые отсекает плоскость на осях Ox, Oy и Oz соответственно.
