13. Однородные слау. Св-ва решений. Фундаментальная система решений однородной слау.

Однородной СЛУ назыв. система, правая часть которой равна нулю: 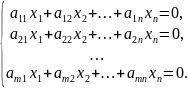Матричный вид однородной системы: Ax=0.

Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение: x1=0 , x2=0 , ..., xn=0.

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

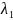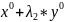Св-во решений. Теорема: Пусть и явл. решениями однородной системы. Пусть , - любые числа. Тогда * + * - тоже явл. решением однородной системы. Док-во: Т.к. , - решение однородной системы, то А* =0, А* =0. А( * ) = А(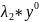 * )+А( ) = *А* + =0 (т.к. А* =0, А* =0). => * - решение однородной системы. Вообще, любая линейная комбинация решений однородной системы – тоже явл. решением этойсистемы.

Т.к. решение ОС – n-мерные вектора, то rg A ≤ n => max число ЛНЗ векторов решения однородной системы – тоже ограничено => из всего бесконечного мн-ва решений однородной системы, можно выделить max ЛНЗ систему, что любое др. решение ОС можно выразить в виде линейной комбинации в-ов этой системы.

Опред.: любая max ЛНЗ система решений ОС назыв. её фундаментальной системой решений.

Очевидно, что n-мерный вектор явл. решением ОС  когда его можно представить в виде линейной комбинации в-ов фундаментальной системы.

14. Метод последовательных исключений Гаусса решения слау.

Метод Гаусса — классический метод решения СЛАУ. Состоит в постепенном понижении порядка системы и исключении неизвестных.

Описание метода

Пусть исходная система выглядит следующим образом

(4)

Тогда согласно свойству элементарных преобразований над строками эту систему можно привести к трапециальному виду:

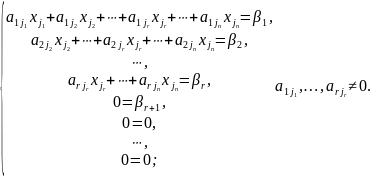
Переменные 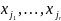называются главными переменными. Все остальные называются свободными.

Если , то рассматриваемая система несовместна.

Предположим, что .

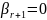Перенесем свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом :

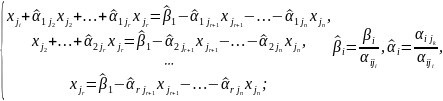(5)

где .

Если свободным переменным системы (5) придавать все возможные значения и вычислить через них главные переменные, то мы получим все решения этой СЛАУ. Так как эта система получена путем элементарных преобразований над исходной системой (4), то по теореме об эквивалентности при элементарных преобразованиях полученное нами решение является решением системы (4).

Следствия

• Если в совместной системе все переменные главные, то такая система является определенной.

• Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределенной, либо несовместной.

Условие совместности

Упомянутое выше условие может быть сформулировано в качестве необходимого и достаточного условия совместности (рангом совместной системы называется ранг ее основной матрицы (либо расширенной, так как они равны).