13.Критерий сходимости в среднем квадратичном.

Лемма. Пусть

Доказательство. Следует из соотношения

и неравенства Шварца для математических ожиданий, которое используется для каждого слагаемого в правой части этого соотношения, например

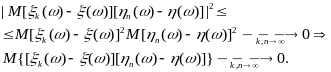
Теорема (критерий сходимости в среднем квадратичном). Для того чтобы последовательность {ξ_k(ω), k=1,2,…} сходилась в среднем квадратичном к некоторой СВ, необходимо и достаточно, чтобы существовал предел:

Доказательство. Необходимость. Пусть

Положим η_n(ω)=ξ_n(ω), тогда по лемме, будем иметь

И в качестве А можно взять Мξ²(ω).

Достаточность. Пусть

следовательно, последовательность {ξ_k(ω), k=1,2,…} является фундаментальной в среднем квадратичном и поэтому сходится в этом смысле

14. Закон больших чисел.

Определение: если

то говорят, что для последовательности СВ {ξ_k(ω), k=1,2,…} выполняется закон больших чисел.

Используя определение сходимости по вероятности , получаем, что в этом случае

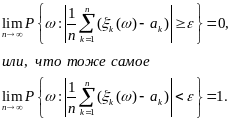
Теор1. Для того чтобы посл-ти СВ {ξ_k(ω), k=1,2,…} выполнялся закон больших чисел, необход и дост, чтобы

Доказательство. Необходимость. Пусть

Отсюда следует, что

Достаточность. Нам дано, что

Рассмотрим следствия из этой теоремы.

Теорема Маркова. Если

То имеет место закон больших чисел.

Это вытекает из соотношения

.

Теорема Чебышева. Если посл-сть независимых СВ {ξ_k(ω), k=1,2,…}, такова, что D{ξ_k(ω)}≤c, k=1,2,…, где с- некоторая константа, то имеет место закон больших чисел.

Это следует из теоремы Маркова и незс-ти СВ, поскольку

15. Усиленный закон больших чисел.

Приведем вспомогательное неравенство, известное как неравенство Гаека-Реньи: пусть {ξ_k(ω), k=1,2,…} последовательность независимых СВ,

Мξ_k(ω)=а_k, Dξ_k(ω)=σ²_k, k=1,2,…. Если с₁,с₂,…-невозрастающая последовательность неотрицательных чисел, то для любых m и n, таких, что m<n, и для любого ε>0

Теорема1.(усиленный закон больших чисел в форме Колмогорова). Пусть {ξ_k(ω), k=1,2,…} последовательность независимых СВ . Тогда для нее выполняется усиленный закон больших чисел, т.е.

Доказательство. В неравенстве Гаека-Реньи положим с_k=1/k и, т.к. оно справедливо для любого n,

В связи с этим, устремляя м к ∞, получаем

Что и доказывает теорему.

Теорема2.(Колмогорова). Пусть {ξ_k(ω), k=1,2,…} последовательность независимых одинаково распределенных СВ. Для выполнения усиленного закона больших чисел необходимо и достаточно существование у СВ конечного математического ожидания.

16. Центральная предельная теорема.

Теорема1.(Линдеберга). Если послед-сть независимых СВ ξ₁(ω),ξ₂(ω),… при τ>0 удовлетворяет усл. Линдеберга:

то при n→∞ равномерно относительно х

Доказательство. Пусть

Условия Линдеберга можно переписать в виде

Характеристическая функция суммы

Где φ_nk(x)-харак-cкая функция СВ ξ_nk. Нам требуется доказать, что , где - хар-ская фун. СВ, распределенной по нормальному закону с параметрами (0,1). Докажем в начале, что равномерно относительно k, 1≤k≤n. Поскольку

Неравенства (4) позволяют получить след. oценку:

Поэтому согласно (3), равномерно в каждом конечном интервале значений t lim_n→∞(ρ_n)=0(5). Таким образом, из

и (5) следует, что что и требовалось док.