
- •1. Классическое и геометрическое определение вероятности, элементы комбинаторики
- •2. Аксематическое определение вероятности. Свойства вероятности.
- •3. Формула полной вероятности. Формула Байеса.
- •4. Схема независимых испытаний Бернулли. Предельная теорема Пуассона.
- •5. Классификация случайных величин.
- •2) Непрерывные случайные величины.
- •6. Математическое ожидание и его свойства.
- •7. Дисперсия и ее свойства.
- •Свойства дисперсии:
- •8. Характеристические функции и их свойства.
- •Свойства характеристической функции :
- •Способы описания св:
- •9.Теорема об обращении характеристической функции.
- •1 1. Виды сходимости случайных последовательностей.
- •13.Критерий сходимости в среднем квадратичном.
- •15. Усиленный закон больших чисел.
- •16. Центральная предельная теорема.
- •10.Производящие функции и их свойства.
- •17. Определение случайного процесса.
- •19. Статистические средние характеристики случайных процессов.
- •20. Сходимость в среднем квадратичном для случайных процессов.
- •21. Непрерывность случайных процессов.
- •22. Дифференцируемость случайных процессов.
- •23. Интегрирование случайных процессов.
- •24. Стохастические обыкновенные дифференциальные уравнения.
- •25. Процессы с независимыми приращениями.
- •26. Гауссовский случайный процесс.
- •27. Винеровский случайный процесс.
- •28. Марковские случайные процессы и цепи маркова определения.
- •29. Однородные цепи Маркова.
- •32. Уравнения Чепмена-Колмогорова.
- •33. Нахождение вероятностей переходов с помощью производящих функций.
- •34. Классификация состояний цепи Маркова по арифметическим свойствам вероятностей перехода
- •35. Свойство периода состояния.
- •36. Классификация состояний по асимптотическим свойствам переходных вероятностей
- •37. Критерий возвратности состояний.
- •38.Эргодические цепи Маркова
- •40. О средних временах переходов между состояниями
- •41. Стационарные цепи Маркова
- •42. Оптимальные стратегии в марковских цепях
- •43. Система диф.Ур-ий Колмогорова для однородной цепи Маркова с конеч.Числом состояний.
- •44. Процесс гибели и размножения
- •49. Обобщенное уравнение Маркова
- •50.Диффузионные процессы
- •51. Обратное уравнение Колмогорова
- •45. Марковские системы массового обслуживания.
- •Рассмотрим систему с простейшим потоком и экспоненциальным обслуживанием
- •46. Система обслуживания м / м / 1
- •47.Система м / м / n / 0
- •48. Система обслуживания м / м / n
- •52.Прямое уравнение Колмогорова для диффузных процессов
- •53. Стохастический интеграл Ито
- •54. Стохастический интеграл в форме Стратоновича
- •55. Стохастические дифференциальные уравнения
- •39. Закон больших чисел для цепей Маркова с конечным числом состояний.
- •57. Стационарность гауссовского случ.Процесса.
- •58. Теорема Бохнера., спектральная плотность случ.Процесса.
- •60. Мартингалы.
- •18. Пуассоновский случ.Процесс
- •Классическое и геометрическое определение вероятности, элементы комбинаторики
51. Обратное уравнение Колмогорова
Т.1.
Пусть
существуют непр-ные частные производные
1-го и 2-го порядков
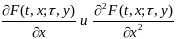 при любых значениях
при любых значениях
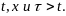 И
пусть выполнены условия (12.5)-(12.7). Тогда
функция
удовлетворяет
уравнению
И
пусть выполнены условия (12.5)-(12.7). Тогда
функция
удовлетворяет
уравнению
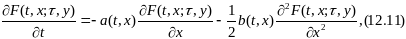 которое
называется обратным
уравнением Колмогорова.
которое
называется обратным
уравнением Колмогорова.
Д-во. Заменив в обобщенном уравнении Маркова
(12.3)
t
на
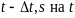 и
используя условие нормировки для ф.р.,
получим
и
используя условие нормировки для ф.р.,
получим
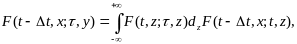
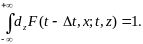
Тогда
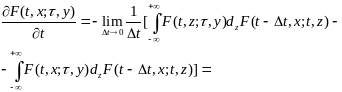
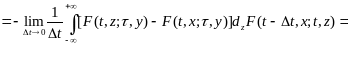
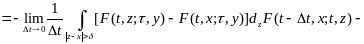
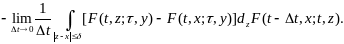 (12.12)
(12.12)
При сделанных нами предположениях по формуле Тейлора имеет место равенство
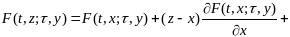
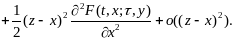
Тогда, подставляя это выражение в (12.12) и используя (12.5) (12.7), далее будем иметь
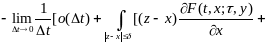
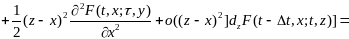
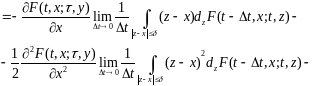
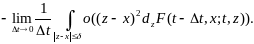 (12.13)
(12.13)
Последнее
слагаемое стремится к нулю при
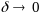 .
Но т.к. левая часть равенства (12. 12) от
(12.5) не зависит и пределы (12.6) и (12.7) также
от 8 не зависят, выражение (12.13) существует
и равно
.
Но т.к. левая часть равенства (12. 12) от
(12.5) не зависит и пределы (12.6) и (12.7) также
от 8 не зависят, выражение (12.13) существует
и равно
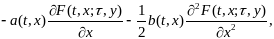
что и приводит нас к уравнению (12.11).
где
(12.5)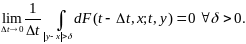 (12.7)
(12.7)
30. Простейший поток событий.
Простейшим (Пуасоновским) потоком событий называется поток обладающий следующими тремя свойствами
А) Стационарность (вероятность появления k-событий на любом промежутке времени зависит только от числа событий k и от длительности промежутка времени и не зависит от начала и конца отсчета времени).
В) Отсутствие последействия (вероятность появления события на любом промежутке времени не зависит от того появились или не появились события в моменты времени предшествующие началу рассматриваемого промежутка)
С) Ординарность (появление двух или более событий за малый промежуток времени практически не возможно)
Интенсивностью
потока
называется
среднее число событий простейшего
потока за время t
определяется по формуле Пуассона
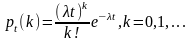
Отображает все свойства простейшего потока.
Свойства А, В выполняются т.к. в формуле не используется информация о появлении событий до начала рассматр. промежутка.
45. Марковские системы массового обслуживания.
Пусть
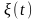 -число
заявок в системе в момент времени t
. Вероятностное распределение
- после момента t
определяется
-число
заявок в системе в момент времени t
. Вероятностное распределение
- после момента t
определяется
А)числом заявок в момент t
б) моментами поступления заявок после момента t и
в) моментами окончания оьслуживания заявок после момента t
Рассмотрим систему с простейшим потоком и экспоненциальным обслуживанием

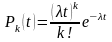
В силу отсутствия памяти у экспоненциального распределения, моменты поступления заявок после момента t не зависят от предистории системы до момента t. Аналогично моменты окончания обслуживания заявок после момента t так же не зависят от предистории системы до момента t.
П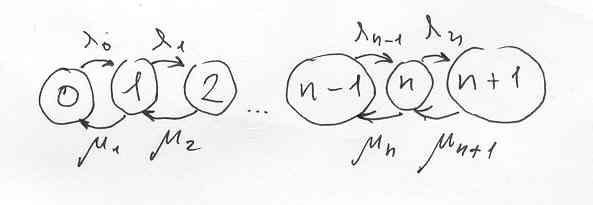 оэтому
вероятное поведение процесса
оэтому
вероятное поведение процесса
 после момента t
зависит только от
и не зависит от поведения
до момента t
. Поэтому
-марковский процесс с конечным или
счетным числом состояния
после момента t
зависит только от
и не зависит от поведения
до момента t
. Поэтому
-марковский процесс с конечным или
счетным числом состояния
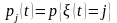
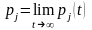
В большинстве рассмотренных моделей -процесс гибели и размножения с графом переходов
Ур-ния для стационарных вероятностей состояний (ур-ния равновесий)
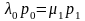 (1)
(1)
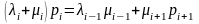 i=1,2...
(2)
i=1,2...
(2)
Из
(2) при i=1
отнять соотн. (1) получим
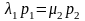
Если из (2) при i=2 отнять последнее то получим
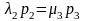
...
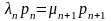 n=0,1,2...
(3)
n=0,1,2...
(3)
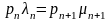
Параметр
экспоненциального распределения
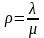 ,
времени обслуживания заявок,
,
времени обслуживания заявок,
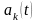 -
обозначим вероятность поступления
k-заявок
за время t,
-
обозначим вероятность поступления
k-заявок
за время t,
 -вероятность
поступления двух и более заявок за время
t.
-вероятность
поступления двух и более заявок за время
t.
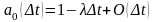 (4)
(4)
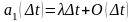 (5)
(5)
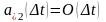 (6)
(6)
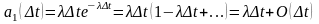
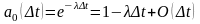
-вероятность поступления заявок
 рассмотрим
однолинейную систему масс.обсл.
рассмотрим
однолинейную систему масс.обсл.
 (за
время t
будет обслужено k
заявок, что
в момент t
обслуживается
некот.
заявок)
(за
время t
будет обслужено k
заявок, что
в момент t
обслуживается
некот.
заявок)
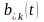 -обозначим
аналогичную вероятность обслуживания
k
и более заявок
-обозначим
аналогичную вероятность обслуживания
k
и более заявок
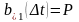 (время
обслуживания 1 и более заявок будет
меньше либо равно
(время
обслуживания 1 и более заявок будет
меньше либо равно
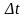 )
)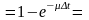
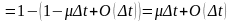
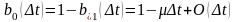 (7)
(7)
Если
бы линия работала непрерывно, то моменты
окончания обслуживания заявок образовывали
бы простейший поток с параметром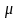 ,
и вероятность
,
и вероятность
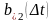 которую
при данном предположении
которую
при данном предположении
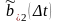 была бы в силу одинарности равна
была бы в силу одинарности равна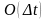
За
маленький промежуток времени обслуживаются
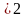 заявок
заявок
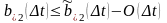 (8)
(8)
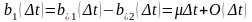
 (9)
(9)
Рассмотрим n-линейную СМО
линии работают независимо друг от друга
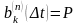 (за
время
будет
обслужено k
заявок)
(за
время
будет
обслужено k
заявок)
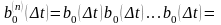
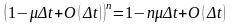 (10)
(10)
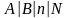
А- входящий поток заявок, N- количество мест для ожидания системы
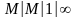
М-входящий поток заявок простейший, Вторая М-обслуживание является экспоненциальным, 1- однолинейная
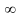 -
неограниченное число мест,
-число
заявок системы в момент времени t
-
неограниченное число мест,
-число
заявок системы в момент времени t
Определим вероятности перехода для
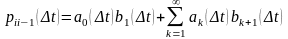
из
(4),(9),(8)
 ,
,
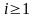
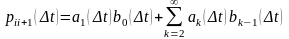
из
(5),(7),(6)
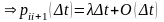
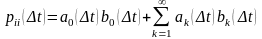
из
(4),(7)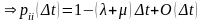 ,
,
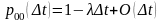
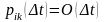 ,
,
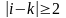
-коэфициент загрузки системы
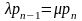 ,
n=1,2...
,
n=1,2...
где
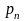 -
вероятность того, что в стац. сост.
решение наход. n-заявок
-
вероятность того, что в стац. сост.
решение наход. n-заявок
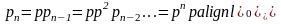
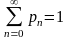 ;
;
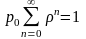
,
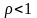
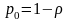
 ,
n=0,1,2...
(13)
,
n=0,1,2...
(13)
При рассмотрении послед. систем МО выражение для переход. вероятностей находятся таким же образом соотнош.(4)-(12) поэтому в дальнейшем мы будем изобр. граф перехода для соотв. процесса гибели и размножения.
31.Пуассоновский случайный процесс как однородная цепь Маркова с непрерывным временем.
Покажем,
что пуассоновский процесс является
цепью Маркова. В силу отсутствия
последствия
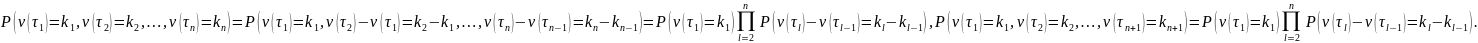
Поэтому,
используя определение условной
вероятности, имеем: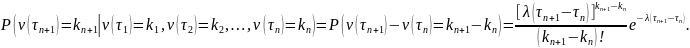
Кроме
того, получим: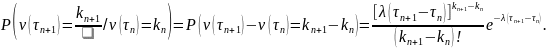
Таким
образом,
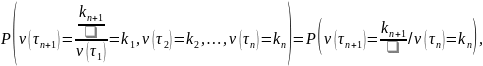 значит,
значит,
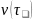 -цепь
Маркова.
-цепь
Маркова.
