2. Знаходження наслідків з даних посилок

Відповідь на питання, як можна знаходити всі формули, які є наслідками даної сукупності формул дає наступна теорема.

Теорема 6. 1. Формула , яка не є тавтологією, тоді й тільки тоді буде логічним наслідком формул , не всі із яких є тавтологіями, коли всі ДЕД з подання формули Н в вигляді ДКН-форми входять в ДКН-форму формули .

Алгоритм знаходження всіх формул, які є логічними наслідками посилок .

1. скласти кон’юнкцію ;

2) знайти ДКН-форму формули ;

2. виписати всі ДЕД знайденої ДКН, а також усі можливі кон’юнкції цих одночленів. Одержана множина формул і є шуканою.

3. Знаходження посилок для даного наслідку.

Теорема 6.2. Щоб знайти всі формули, логічним наслідком кожної з яких є , потрібно

1. знайти ДКН-форму для форму­ли ;

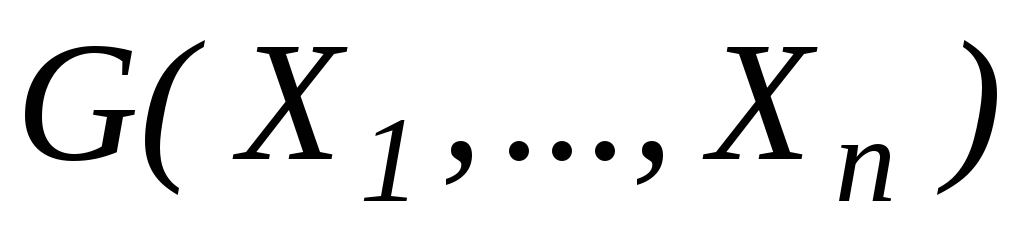2. визначити всі ДЕД які в ній відсутні;

3. скласти всі можливі кон’юнкції формули з ЕД, яких не вистачає. Одержана сукупність формул (разом з формулою G) буде шуканою ( з точністю до рівносильності формул).

Виведення (вивід)  це логічна (розумова) операція, яка полягає в одержанні нового твердження із одного або декількох раніше відомих тверджень. Виведення діляться на дедуктивні й індуктивні. Широко відомою є думка про те, що дедуктивне виведення  це виведення “від загального до окремого”, а індуктивне  “від окремого до загального”. Але така думка лише в самих загальних рисах характеризує, зокрема, дедуктивне виведення. Ця одна наведена властивість ще не є для них визначальною. Дедуктивні виведення спираються на аналізі формальної (логічної) структури посилок і наслідків, а індуктивні  на аналізі їх змісту.

Правильність дедуктивного виведення означає, що воно приводить до істинного висновку не завжди, але кожного разу, якщо воно виходить із істинних посилок.

Щоб установити неправильність виведення, потрібно указати таку його конкретизацію (приклад), де усі посилки були б істинними, а наслідок був би хибним.

Лекція 7 План

1. Числення висловлень

1. Числення висловлень

У загальному вигляді формальна теорія Т, яка ще називається численням, будують таким чином.

1. Означають набір основних символів  алфавіт теорії.

2. Конструктивно означають множину формул, або правильно побудованих виразів, яка утворює мову теорії.

3. Виокремлюють підмножину формул, які називають аксіомами теорії.

4. Задають правила виведення (виводу) теорії.

Розглянемо один із варіантів числення висловлень, яке називатимемо ЧВ.

Алфавіт ЧВ складається з пропозиційних змінних Х₁, Х₂, ..., Х_п, знаків логічних операцій і технічних знаків ( , )  круглих дужок.

Поняття формули ЧВ означається наступним чином.

1. Кожна пропозиційна змінна є формула.

2. Якщо F₁ , F₂  формули, то вирази також є формулами.

3. Інших формул, ніж побудованих за правилами 1 і 2 немає.

Аксіоми ЧВ.

(А1): ;

(А2): ;

(АЗ):

де F, G, Н  довільні формули.

Правилом виведення в ЧВ є правило тdиs ропеns, (МР): із формул F і F G безпосередньо випливає формула G. Це правило будемо записувати у вигляді: МР(F₁, F₁ G)=G .

Кожен із виразів (А1), (А2), (АЗ) задає лише форму аксіоми, а тому називається схемою аксіом.

Схема формул  це вираз метамови для позначення нескінченної множини всіх тих формул числення, які отримуються після заміни змінних метамови (метазмінних) цієї схеми певними формулами числення.

Якщо у вивідній формулі F(P), яка містить літеру Р, замінити усі входження Р на довільну формулу Q, то формула F(Q) є також вивідною. Таку заміну далі позначатимемо .

Для скороченого запису формул вводяться зв’язки , які означаються так:

означає ;

означає; ;

означає .

Означення 7.1. Виведенням формули F із множини формул Г називається така скінчена послідовність формул В₁, В₂, …, В_s=F , кожна із якої є або аксіомою, або формулою із Г, або формулою, одержаною із попередніх за допомогою правила виведення. Якщо є вивід формули F із множини формул Г, то говорять що F вивідна із Г, і записують Г├ F. Елементи із Г називають гіпотезами або посилками виводу. Якщо є вивід формули F із пустої множини гіпотез, тобто формула F виводиться лише із аксіом, то таке виведення називається доведенням даної формули, а саму формулу F називають теоремою. Якщо F  теорема, то це записують так ├ F.

Приклад 7.1. Довести F├ F.

В₁:

В₂:

В₃: МР(В₂, В₁)=

В₄: ;

В₅: МР(В₄, В₃)=

Теорема 7.1. (Властивості вивідності).

1. Якщо Г├ F і Г , то Г├ F і ├ F .

2. Г├ F тоді й тільки тоді, коли в Г існує така сканченна підмножина  , що ├ F.

3. Якщо Г├ G для довільної формули G із множини  і ├ F, то Г├ F .

Будь-яке доведене в численні висловлень виведення вигляду Г├ F , де Г множина формул, F  довільна формула, можна розглядати як правило виведення , яке можна додати до заданої множини правил. Такі правила називаються похідними правилами. Могутнім засобом одержання ряду важливих похідних правил виведення є теорема дедукції.

Теорема 7.2 (теорема дедукції).

Якщо F₁, F₂, ..., F_m-1, F_m ├ G , то F₁, F₂, ..., F_m-1├ F_m  G. Зокрема, якщо F├ G, то ├ F G.

Наслідок 7.1. F₁, F₂, ..., F_m-1, F_m ├ G , тоді й тільки тоді, коли

F₁, F₂, ..., F_m-1├ F_m  G.

Доведення. Необхідність випливає з теореми дедукції. Доведемо достатність. Якщо F₁, F₂, ..., F_m-1├ F_m  G, то існує відповідний вивід: , ..., , .

Доповнимо його двома формулами F_т і G. Одержимо послідовність , ..., , F_m  G, F_т , G, яка є виводом формули G із гіпотез, оскільки передостння формула цієї послідовності є однією з гіпотез, а остання одержана з двох попередніх ій формул за правилом МР.

Наслідок 7.2. F₁, F₂, ..., F_m-1, F_m ├ G тоді й тільки тоді, коли

├ F₁  (F₂  ... (F_m-1 (F_m  G))…).

Даний наслідок одержуємо m-кратним застосуванням попереднього наслідку.

За допомогою теореми про дедукцію спочатку доведемо наступну лему, яка потім разом з теоремою про дедукцію використовуватиметься для доведення теорем ЧВ.

Лема 7.1. Для будь-яких формул F, G, Н справедливі наступні виведення:

а) ├ FH;

б) G ├ FH.

Доведення. а) Покажемо спочатку, що , F ├ H. Для цього побудуємо послідовність, яка є відповідним виводом: ,F, G,, Н. Перші три формули послідовності суть гіпотези. Четверта фор­мула G одержана з першої й третьої формул послідовності за правилом МР, а п’ята  із другої й четвертої за тим же правилом. Отже , F ├ H. Звідси за теоремою про дедукцію робимо висновок ├ FH.

б) Неважко бачити, що G, F ├ H, звідки за теоремою про дедукцію маємо G ├ FH.

Приклад 7.2. Довести теорему .

В₁: ,

В₂: (Приклад 7.1) = ,

В₃: Лема 7.1(б) = ,

В₄: ,

В₅: Лема 7.1(б) = .

Послідовність формул В₁, В₂, В₃, В₄, В₅ не є виводом формули із аксіом. Це виведення ґрунтується не лемі 7.1, яка в свою чергу спирається на теорему дедукції.