Приклад. Нехай p (n)  “n ділиться на 6”, q (n)  “n ділиться на 3”, тоді p  q .

Із наведених означень випливає: PQ тоді й тільки тоді, коли P  Q і Q  P .

Мають місце наступні теореми.

Теорема 9.1. Кожні два тотожно істинні (тотожно хибні) предикати задані на одних і тих же множинах рівносильні між собою. Будь який предикат, рівносильний тотожно істинному (тотожно хибному), сам є тотожно істинним ( тотожно хибним) предикатом.

Теорема 9.2. Кожен тотожно істинний n-місний предикат є наслідком будь якого другого n-місного предикату, визначеного на тих же множинах. Кожен n-місний предикат є наслідком будь якого другого тотожно хибного n-місного предикату, визначеного на тих же множинах.

Теорема 9.3. Нехай і два n-місних предикати, визначених на одних і тих же множинах і . Тоді:

а) якщо тотожно істинний (виконуваний), то і тотожно істинний (виконуваний);

б) якщо тотожно хибний (спростовний) то і тотожно хибний (спростовний).

Доведення.

а) Оскільки , то Р⁺ Q⁺. Якщо Р тотожно істинний предикат, то (де М₁, М₂, ..., М_п  множини на яких визначені п-місні предикати Р і Q). Але . Тому , отже, Q  тотожно істинний. Якщо Р  виконуваний предикат, то Р⁺ ≠ Ø. Але Р⁺ Q⁺. Тоді Q⁺ ≠ Ø і Q  виконуваний предикат.

б) Нехай Q  тотожно хибний предикат. Тоді Q⁺ = Ø. Оскільки Р⁺Q⁺, то Р⁺=Ø. Отже, предикат Р  тотожно хибний. Нехай тепер Q  спростовний предикат. Тоді . Оскільки, крім того, Р⁺Q⁺ и , то . Отже, предикат Р  спростовний.

Попередні дві теореми доводяться аналогічно останній.

Лекція 10

План

1. Логічні операції над предикатами.

2. Кванторні операції над предикатами.

3. Обмежені квантори.

1. Логічні операції над предикатами

Заперечення предиката. Запереченням п-місно­го предиката , визначеного на множинах М₁, М₂, ..., М_п, називається п-місний предикат ¬, який перетворюється в істинне висловлення при всіх тих і тільки тих значеннях предметних змінних, при яких вихідне висловлення перетворюється в хибне висловлення.

Теорема 10.1. Для п-місно­го предиката , визначеного на множинах М₁, М₂, ..., М_п, множина істинності його заперечення збігається з доповненням його множини істинності, тобто .

Тут мається на увазі, що доповнення розглядається в множині , тобто .

Доведення.

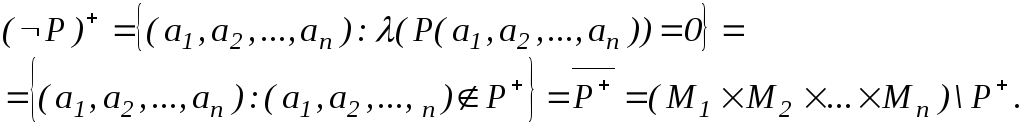
Зауваження. Згідно наведеного означення, запереченням предиката є будь-який із рівносильних предикатів, котрий задовольняє даному означенню. Наприклад, запереченням предиката “” на множині R є кожний із наступних предикатів: “”, “”, “”.

Це зауваження потрібно мати на увазі й при розгляді інших логічних операцій.

Кон’юнкція двох предикатів. Кон’юнкцією п-місного предиката , визначеного на множинах М₁, М₂, ..., М_п, і т-місного предиката , визначеного на множинах N₁, N₂, ..., N_т, називається (п + т)-місний предикат , визначений на множинах М₁, М₂, ..., М_п, N₁, N₂, ..., N_т, який перетворюється в істинне висловлення при всіх тих і тільки тих значеннях предметних змінних, при яких обидва дані предикати перетворюються в істинне висловлення.

Іншими словами, предикат такий, що для довільних предметів , , ..., , , , ..., маємо висловлення .

Операцію кон’юнкції можна застосувати до предикатів, які мають спільні змінні. У цьому випадку в новому предикаті число змінних рівне числу п + т - k, де п  число змінних першого предиката, т  число змінних другого предикати, k  число спільних змінних для обох предикатів.

Якщо обидва предикати визначені на одних і тих же множинах і залежать від одних і тих же змінних, то для них справедлива наступна теорема.

Теорема 10.2. Для п-місних предикатів і , визначених на множинах М₁, М₂, ..., М_п, множина істинності кон’юнкції збігається з перерізом множин істинності вихідних предикатів: .

Наслідок. Кон’юнкція двох предикатів тотожно істина тоді й тільки тоді, коли обидва дані предикати тотожно істинні.

Диз’юнкція двох предикатів. Диз’юнкцією п-місного предиката , визначеного на множинах М₁, М₂, ..., М_п, і т-місного предиката , визначеного на множинах N₁, N₂, ..., N_т, називається (п + т)-місний предикат , визначений на множинах М₁, М₂, ..., М_п, N₁, N₂, ..., N_т, який перетворюється в істинне висловлення при всіх тих і тільки тих значеннях предметних змінних, при яких в істинне висловлення перетворюється принаймні один із даних предикатів.

Тобто, предикат такий, що для довільних предметів , , ..., , , , ..., маємо висловлення .

Теорема 10.3. Для п-місних предикатів і , визначених на множинах М₁, М₂, ..., М_п, множина істинності диз’юнкції збігається з об’єднанням множин істинності вихідних предикатів: .

Наслідок. Диз’юнкція двох предикатів є виконуваним предикатом тоді й тільки тоді, коли принаймні один з двох предикатів є виконуваним.

Наслідок. Диз’юнкція двох предикатів тотожно хибна, коли обидва дані предикати тотожно хибні

Доведення наведених теорем і наслідків ґрунтуються на відповідних означеннях й аналогічні доведенню теореми 10.1.

Виникає питання, які закономірності утворення рівносильних предикатів за допомогою уведених операцій? Аналогічне питання виникає й стосовно наслідку предикатів.

Відповідь на це дає наступна теорема.

Теорема 10.4. Якщо в усіх формулах, що виражають властивості кон’юнкції й диз’юнкції алгебри висловлень ( див. лекцію 2) під Р, Q, R розуміти предикати визначені на відповідних множинах, знак ↔ всюди замінити знаком , а знак →  знаком , то одержимо справедливі твердження про предикати.

Дана теорема безпосередньо випливає із означення рівносильності предикатів.