3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм
Для оценки погрешности (разности
векторов точного и приближенного
решений) используются различные нормы
линейного векторного пространства.
Напомним, что нормой вектора
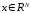называется произвольный линейный
положительно определенный функционал
,
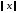который
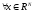удовлетворяет
трем аксиомам:
1.
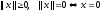– положительная определенность;
2.
,
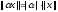– линейность при умножении на скаляр;
3.
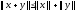– неравенство треугольника.
Векторные нормы, получившие наиболее широкое распространение в численном анализе:
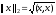– Евклидова норма (при соответ-м
определении скалярного произведения);
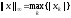– максимальная норма;
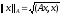– энергетическая норма, порожденная
положительно определенным самосопряженным
оператором
.
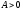Т.к. для матриц определена операция
умножения, то естественно добавить
требовавание
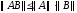– аксиома мультипликативности
матричной нормы.
Матричная норма называется согласованной,
если
(вектор
в данном случае может трактоваться как
матрица, имеющая размерность
).
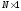Для получения не улучшаемых оценок
произведения матрицы на вектор используют
нормы матриц, подчиненные соответствующим
векторным нормам.
Определение.
Норма матрицы
,
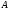подчиненная векторной норме
,
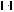определяется числом
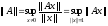(1)
В случае квадратных матриц из определения подчиненной матричной нормы следует ее согласованность, мультипликативность и минимальность среди всех возможных согласованных норм. Подчиненные матричные нормы для приведенных выше основных векторных норм вычисляются следующим образом.
–
матричная норма, подчиненная векторной
Евклидовой норме, равна максимальному
сингулярному числу матрицы.
Сингулярные числа матрицы вычисляются
как корень квадратный из совпадающих
собственных значений матриц
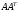и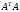
.
Для симметричной, положительно
определенной матрицы сингулярные числа
совпадают со спектром собственных
значений данной матрицы.
.
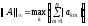В качестве данной нормы выступает
максимальное значение суммы абсолютных
величин элементов строк матрицы.
Выбор конкретной нормы для получения оценок приближенного решения определяется в основном целью исследований и спецификой задачи. При этом следует иметь в виду, что нормы конечномерного линейного векторного пространства эквивалентны с точностью до постоянного множителя.
Норма
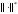эквивалентна норме
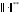если для любого элемента
(вектора или матрицы) найдутся такие
постоянные
и
,
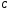что выполняется неравенства
.
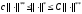Например, для норм
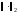и
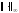имеют место оценки
,
.
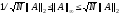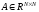3.2. Методы Рунге-Кутта. Схема метода четвертого порядка.
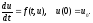(1)
Приближенное
решение находиться в виде
,
(2), где
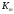имеют вид
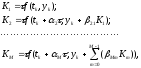(3)
,
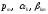выбираются из соображений точности.
Например такие, чтобы при минимальном
значении
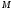обеспечить
максимальный порядок малости локальной
ошибки (погрешности дискретизации).
Для простоты рассмотрим случай M=2, для которого подстановка (3) в (2) дает:
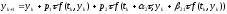(4)
В
(4) подставим вместо
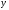точное решение дифф. з-чи (1)
,
полагая, что решение дифф. задачи известно
в точке
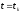и м. б. представлено конечным отрезком
степенного ряда в
-окрестности
данной точки. Это требование означает
непр. дифф-ть и ограниченность производных
решения до некоторого необходимого
порядка. Потребуем также непр. дифф-ть
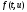по всем ее аргумента в точке
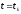и
-окрестности
текущего узла.
Для подстановки точного решения в формулу Р-К (4) используем следующие выражения:
,
.
.
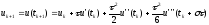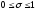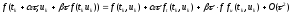Здесь
нижние индексы функции
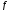означают
частные производные по соответствующим
аргументам. Осуществляя подстановку
этих представлений в формулу (4), приходим
к:
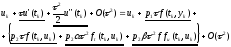
Полученное
выражение, после приведения подобных
и деления на
,
можно переписать:
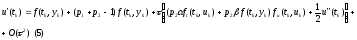Подстановка
точного решения в схему Р-К даёт в опр-м
смысле эквивалентность данной схемы и
некоторой новой дифф. задачи, которая
получается из исходной задачи Коши
добавлением в правую часть уравнения
некоторых "возмущающих" членов,
связаные с переходом от дифф. задачи к
дискретной модели. Совокупность всех
возмущений, обусловленных переходом
от дифф. задачи к дискретной модели,
принято называть погрешность
аппроксимации (дискретизации)
или невязка. Величина
данных возмущений будет определять
отличие решений исходной и возмущенной
задач. Но погрешность аппроксимации
это еще не погрешность решения, а ее
основной источник.
Определим, при каких
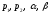достигается min локальной
погрешности схемы Рунге-Кутты как
дискретной модели задачи Коши. Для этого
потребует, чтобы
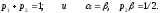(6)
Заметим, что первое из уравнений (6) гарантирует равенство нулю первого возмущающего члена в выражении (5), а два последних – второго. Несложно показать, что последний возмущающий член в (5) при выполнении условий (6) никогда не равен нулю.
Но условия (6) не дают однозначного
определения коэффициентов. Например,
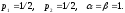соответствует методу Эйлера-Коши.
В рамках схемы (4) определяется однопараметрическое семейство методов Рунге-Кутты второго порядка аппроксимации, коэффициенты при этом выражаются зависимостью от некоторого свободного параметра:
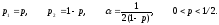
Наибольшую популярность получил метод Рунге-Кутты четвертого порядка
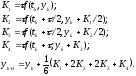(7)
Для схем более высоких порядков также характерна неоднозначность. Например, одним из вариантов схем Рунге-Кутты четвертого порядка является следующая схема:
(7')
Выражения для коэффициентов схем вида
(7) получаются аналогично (обнуление
"возмущающих" слагаемых до
максимально возможного порядка малости
по
).
Естественно, что вычисления усложняются
с повышением порядка схемы, для чего
требуется учитывать все больше и больше
членов в представлении решения отрезком
степенного ряда.
Заметим, что в методах Рунге-Кутты до четвертого порядка аппроксимации включительно количество вычислений функций правой части дифференциальной задачи совпадает с порядком аппроксимации, т.е. вычислительные затраты растут пропорционально порядку аппроксимации. Четвертый порядок аппроксимации не является пределом возможностей методов Рунге-Кутты.
Однако для получения схемы (2) - (3) от пятого до седьмого порядков аппроксимации требуется количество вычислений функции правой части на одно больше чем порядок аппроксимации. Дальнейшее увеличение порядка аппроксимации сопровождается еще более непропорциональным ростов вычислительных затрат. Кроме того, достижение большего порядка аппроксимации сопряжено с требованием большей гладкости решения, т.е. наличием ограниченных производных решения более высокого порядка. По этой причине целесообразность использования методов Рунге-Кутты выше четвертого порядка представляется, вообще говоря, проблематичной.