
- •1.1. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса (вычислительная сложность, выбор ведущего элемента).
- •1.2. Понятие об одношаговых и многошаговых методах. Метод Эйлера решения задачи Коши для системы оду первого порядка.
- •2.1. Lu представление матрицы. Обращение матриц и вычисление определителя.
- •2.2. Локальная и глобальная ошибка одношагового метода решения задачи Коши. Задача для погрешности метода, устойчивость и сходимость.
- •3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм
- •3.2. Методы Рунге-Кутта. Схема метода четвертого порядка.
- •Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лау
- •Многошаговые методы. Явные и неявные методы. Метод Адамса
- •5.1. Понятие устойчивости численных методов для жестких систем. Метод Гира.
- •5.2. Итерационные методы решения систем лау. Метод простой итерации. Условия сходимости и критерий остановки итераций.
- •6.2. Разностная аппроксимация дифференциальных операторов. Сеточный шаблон. Явные и неявные схемы для нестационарных задач математической физики.
- •7.1. Прямые методы вычисления собственных значений. Преобразования подобия. Метод Данилевского.
- •7.2. Порядок аппроксимации разностной схемы. Оценка порядка аппроксимации разностной схемы с весами для нестационарного уравнения теплопроводности.
- •8.1. Оптимальное значение итерационного параметра. Метод минимальных невязок.
- •8.2. Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.
- •9.1. Итерационные методы решения проблемы собственных значений. Степенной метод.
- •9.2. Спектральный метод исследования устойчивости разностных схем для уравнений с постоянными коэффициентами.
- •10.1. Итерационные методы решения нелинейных уравнений. Метод Ньютона.
- •10.2. Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
- •21.1. Спектр собственных значений разностного оператора второй производной.
- •21.2. Разностные аналоги формул Грина и теоремы вложения норм сеточных функций.
9.1. Итерационные методы решения проблемы собственных значений. Степенной метод.
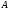 порядка - квадратная невырожденная
матрица
порядка - квадратная невырожденная
матрица
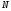 .
.
Число
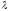 называется собственным значением
матрицы
называется собственным значением
матрицы
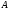 ,
если существует такой ненулевой вектор
,
если существует такой ненулевой вектор
 ,
удовлетворяющий равенству
,
удовлетворяющий равенству
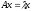 (1)
(1)
Вектор
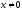 ,
удовлетворяющий равенству (1), называется
собственным вектором матрицы
,
удовлетворяющий равенству (1), называется
собственным вектором матрицы
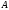 .
Совокупность всех собственных значений
называется спектром матрицы.
.
Совокупность всех собственных значений
называется спектром матрицы.
Уравнение
(1) имеет нетривиальные решения 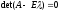 (2)
(2)
Функция
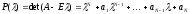 - характеристический многочлен
матрицы. Множество его корней совпадает
со спектром.
- характеристический многочлен
матрицы. Множество его корней совпадает
со спектром.
Степенной
метод: Пусть нужно найти макс. по
модулю собственное значение
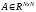 ,
причем, искомое собственное значение
простое. Пусть
,
причем, искомое собственное значение
простое. Пусть
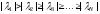 .
.
Заметим, что при умножении матрицы на
ее собственный вектор последний
преобразуется в коллинеарный вектор
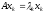 ,
причем длина полученного при этом
вектора изменяется пропорционально
соответствующему собственному значению
,
причем длина полученного при этом
вектора изменяется пропорционально
соответствующему собственному значению
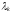 .
Данное свойство собственных векторов
лежит в основе степенного метода.
У матриц простой структуры система
собственных векторов образует базис в
.
Данное свойство собственных векторов
лежит в основе степенного метода.
У матриц простой структуры система
собственных векторов образует базис в
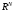 ,
любой вектор может быть представлен:
,
любой вектор может быть представлен:
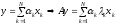 => в разложении по собственным векторам
при умножении матрицы на вектор наибольший
рост (наименьшее убывание) испытывает
составляющая, соответствующая
максимальному собственному значению.
Рассмотрим последовательность
=> в разложении по собственным векторам
при умножении матрицы на вектор наибольший
рост (наименьшее убывание) испытывает
составляющая, соответствующая
максимальному собственному значению.
Рассмотрим последовательность
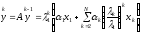 (3)
(3)
Т.к.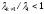 ,
то при
,
то при
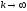
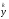 сходится к собственному вектору
сходится к собственному вектору
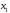 .
Компоненты вектора
.
Компоненты вектора
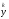 ,
соответствующие другим собственным
значениям стремятся к нулю со скоростью
ГП. Скорость сходимости последовательности
определяется отношением
,
соответствующие другим собственным
значениям стремятся к нулю со скоростью
ГП. Скорость сходимости последовательности
определяется отношением
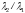 – знаменателем геометрической прогрессии
самой медленной из компонент
– знаменателем геометрической прогрессии
самой медленной из компонент
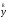 .
.
Заметим, что асимптотика
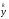 определяется также значением
определяется также значением
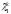 ,
которое в пределе
,
которое в пределе
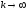 стремиться к нулю или бесконечности, в
зависимости от
стремиться к нулю или бесконечности, в
зависимости от
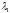 => нужна нормировка промежуточных
результатов. В качестве нормировочного
коэффициента наиболее подходящий выбор
–
=> нужна нормировка промежуточных
результатов. В качестве нормировочного
коэффициента наиболее подходящий выбор
–
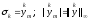 (
(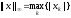 )
=>
)
=>
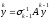 (4)
(4)
Использование итерационной процедуры (4) позволяет определить как собственный вектор, соответств-й макс собств. значению, так и величину собств. значения
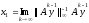 , (5)
, (5)
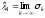 .
(6)
.
(6)
После того как наибольшее собственное значение определено, данный подход может быть использован для вычисление других собственных значений и собственных векторов.
Недостаток степенного метода: не может быть использован в случае, когда матрица имеет равные по модулю собственные значения. Итерационный процесс (4) в этом случае не сходится.
Есть возможность находить степенным методом комплексные характеристические числа и соответствующие инвариантные подпространства для вещественных матриц.
9.2. Спектральный метод исследования устойчивости разностных схем для уравнений с постоянными коэффициентами.
Произвольное частное решение дискретной
задачи ищется в виде
 Подстановка такой
сеточной функции в разностное уравнение
позволяет определить, при каких
Подстановка такой
сеточной функции в разностное уравнение
позволяет определить, при каких
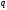 данная сеточная функция удовлетворяет
разностному уравнению.
данная сеточная функция удовлетворяет
разностному уравнению.
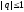 для
для
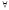 действительных
действительных
 - решение устойчивое.
- решение устойчивое.

 :
:
 -
частное решение неограниченно возрастает
при
-
частное решение неограниченно возрастает
при
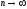 -
неустойчивое.
-
неустойчивое.
Спектральный метод (метод гармоник) позволяет получить необходимые условие устойчивости дискретных моделей. Выяснение вопроса о достаточности полученных условий устойчивости анализируемой схемы требует доказательства полноты системы линейно независимых решений, используемых в качестве пробных сеточных функций при спектральном анализе устойчивости. Естественными краевыми условиями для спектрального метода являются периодические либо однородные граничные условия.
В этом случае пространственные гармоники, используемые в качестве пробных функций, совпадают с собственными функциями дифференциальных и разностных операторов с постоянными коэффициентами.
Собственные функции, удовлетворяющие однородным краевым условиям, образуют ортогональный базис в соответствующем пространстве сеточных функций. В силу этого полученные в рамках спектрального подхода необходимые условия устойчивости являются одновременно и достаточными.
Если разностная задача имеет краевые условия, отличные от однородных либо периодических, то спектральный метод оставляет открытым вопрос об устойчивости данной разностной задачи относительно возмущений таких краевых условий. Этот недостаток спектрального метода вряд ли можно признать существенным, поскольку возмущения краевых условий дискретной модели, как правило, не имеют катастрофических последствий на поведении приближенного решения, если таковые отсутствуют в исходной дифференциальной задаче.
Пример 1. Исследовать устойчивость по начальным данным явной схемы:
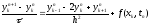 ,
,
Будем
искать частное решение разностной
задачи в виде
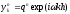 .
Подстановка данного решения в разностную
схему при
.
Подстановка данного решения в разностную
схему при
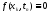 дает следующее равенство
дает следующее равенство
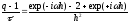 ,
,
откуда
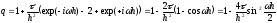 .
.
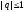 при условии
при условии
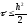 ,
что является необходимым условием
устойчивости рассматриваемой явной
схемы. К такому же результату приводит
спектральный анализ устойчивости данной
схемы с использованием в качестве
пробных функций соответствующие
собственные функции разностного
оператора второй производной с нулевыми
краевыми условиями. Относительно набора
данных собственных функций нами была
установлена их ортогональность и
полнота. Таким образом, спектральный
критерий устойчивости явной разностной
схемы в случае задачи Дирихле с нулевыми
краевыми условиями дает необходимые и
достаточные условия устойчивости
рассмотренной схемы.
,
что является необходимым условием
устойчивости рассматриваемой явной
схемы. К такому же результату приводит
спектральный анализ устойчивости данной
схемы с использованием в качестве
пробных функций соответствующие
собственные функции разностного
оператора второй производной с нулевыми
краевыми условиями. Относительно набора
данных собственных функций нами была
установлена их ортогональность и
полнота. Таким образом, спектральный
критерий устойчивости явной разностной
схемы в случае задачи Дирихле с нулевыми
краевыми условиями дает необходимые и
достаточные условия устойчивости
рассмотренной схемы.
