8.1. Оптимальное значение итерационного параметра. Метод минимальных невязок.

Вычисление оптимального значения итерационного параметра при решении систем линейных алгебраических уравнений требует знания спектра матрицы системы. Определение границ спектра матрицы – непростая задача. Рассмотрим один способ оптимизации итерационного параметра, для которого не требуется симметричность матрицы системы и знание границ её спектра.

Для решения системы ЛАУ 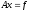с положительно определенной матрицей 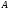используем итерационный метод 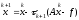(1)

В отличие от метода простой итерации в итерационном процессе (1) используется переменный итерационный параметр. Определим, каким должно быть значение итерационного параметра 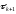, чтобы норма погрешности 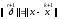для очередного итерационного приближения имела минимальное значение ()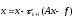

Для погрешности итерационного метода (1) имеем 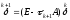(2)

Умножим скалярно уравнение (2) само на себя, предварительно умножив его слева на матрицу :

.

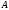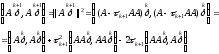Условие минимума нормы погрешности определим из равенства нулю ее производной:

.

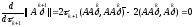Из последнего равенства имеем .

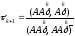Учитывая, что 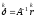, получаем выражение для оптимального значения итерационного параметра 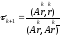, 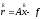(3)

Таким образом, мы приходим к итерационному методу с оптимальным выбором итерационного параметра, обеспечивающего на каждой итерации минимальное значение нормы погрешности 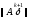: 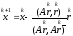(4)

Итерационный метод (4) называется метод минимальных невязок, поскольку 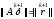и каждая итерация (4) соответствует нахождению следующего приближения, минимизирующего норму невязки .

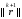Задача выбора оптимального набора итерационных параметров, обеспечивающих минимизацию погрешности решения после 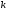итераций, позволяет добиться лучших результатов в ускорении сходимости, нежели рассмотренная выше оптимизация итерационного параметра на каждом итерационном шаге в отдельности.

8.2. Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.

Для численного решения задач по дифференциальным уравнениям методом сеток (конечных разностей) необходимо проделать следующее. Область непрерывного изменения аргумента (аргументов) искомой функции заменяется конечным дискретным множеством точек, называемых узлами сетки. Все производные, входящие в дифференциальную задачу, заменяются разностными производными. Это осуществляется тем или иным методом конструирования разностных схем. В конечном итоге получаем систему алгебраических уравнений. Таким образом, сущность метода сеток состоит в замене исходных дифференциальных задач системами алгебраических уравнений, их приближенно заменяющими.

Если при измельчении шагов сетки решение разностной схемы сходится к решению исходной дифференциальной задачи, то за решение исходной задачи принимается решение разностной схемы. После конструирования разностной схемы необходимо провести теоретические исследования разрешимости задач. Внутренними свойствами разностной схемы являются аппроксимация и устойчивость. Эти свойства разностной схемы должны исследоваться для каждой схемы.

Получающиеся разностные схемы решаются теми или иными методами решения систем алгебраических уравнений. Разрешающий алгоритм должен быть экономичным и этим же требованиям должна обладать и разностная схема.

Сеточная область

Для построения разностной схемы необходимо построить сетку G_h - конечное множество точек, принадлежащих G, плотность распределения которых характеризуется параметрами h-шагом сетки. Пусть область изменения аргумента x есть отрезок G={0≤x≤1}. Разобьем этот отрезок точками x_i=i∙h, i=0,n на n равных частей длины h=1/n каждая. Множество точек x_i=i∙h, называется равномерной сеткой на отрезке 0≤x≤1 и обозначим 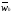={x_i=i∙h, i=0,n} , а число h - расстояние между точками (узлами) сетки называется шагом сетки.

Разбиение отрезка 0≤x≤1 точками x_i, i=0,n можно производить произвольным образом: 0<x₁<…<x_n-1<1. Тогда получаем сетку 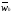={x_i, i=0,n, x₀=0, x_n=1} c шагами h_i=x_i-x_i-1, которые зависит от номера узла сетки. Если h_i≠h_i+1 хотя бы в одной точке, то сетка называется неравномерной и такую сетку обозначают ŵ. Точки x₀ и x_n назовем граничными узлами и обозначим их г_h. Остальные узлы назовем внутренними и обозначим их w_h. Узлы, соседние с граничащими, назовем приграничными. 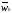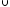Тогда имеем =w_h г_{h .}

Сеточная функция. Пространство сеточных функций. Нормы сеточных функций

Функция y=y(x_i) дискретного аргумента x_i называется сеточной функцией, определенной на сетке 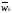. Сеточные функции можно рассматривать как функции целочисленного аргумента, являющегося номером узла сетки, т. е. y=y(x_i)=y(i). Далее мы будем писать y(x_i)=y_i.

Сеточная область w_h зависит от параметра h. При различных значениях параметра h имеем различные сеточные области. Поэтому и сеточные функции y_h(x) зависят от параметра h.

Функции u(x) непрерывного аргумента являются элементами функционального пространства H. Множество сеточных функций y_h(x) образует пространство H_h. Таким образом, в методе сеток пространство H заменяется на H_h сеточных функций y_h(x).

Так как рассматривается множество сеток {w_h}, то мы получаем множество {H_h} пространств сеточных функций, определенных на {w_h}.

Пусть u(x) - решение исходной непрерывной задачи Lu(x)=f(x), (1)

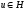; y_h- решение разностной задачи, 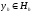. Для теории приближенных вычислений представляет большой интерес оценка близости u(x) и y_h(x), но u(x) и y_h(x) являются элементами из различных пространств. Пространство H отображается на пространство H_h. Каждой функции 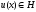ставится в соответствие сеточная функция y_h(x), x w_h, так что y_h=P_hu H_h, где P_h- линейный оператор из H в H_h. Это соответствие можно осуществить различными способами, т. е. зависит от выбора оператора P_h. Теперь, имея сеточную функцию u_h, образуем разность y_h-u_h, которая является вектором пространства H_h.

Близость y_h и u_h характеризуется числом ||y_h-u_h||_Hh , где ||.||_Hh – норма на H_h.

Соответствие функций u(x) и u_h можно установить различными способами, например,

u_h=u(x), x w_h. В дальнейшем мы будем пользоваться этим способом соответствия.

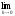
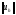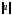В линейном пространстве H_h введем норму ||.||_Hh, которая является аналогом нормы ||.||_Н в исходном пространстве Н. Обычно принято выбирать норму в пространстве H_h так, чтобы при стремлении к нулю h она переходила в ту или иную норму функций, заданных на всем отрезке, т.е. чтобы выполнялось условие: _Hh=_H, (2)

где ||.||_Н - норма в пространстве функций, определенных на отрезке, которому принадлежит решение.

Условие (2) называют условием согласования в пространствах H_h и Н.

Рассмотрим простейшие типы норм в H_h для случая сеток w_h={x_i=i∙h} на отрезке 0≤x≤1.

1. Норма 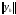_Hh=

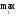
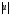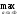
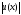удовлетворяет условию (2), если в качестве Н рассматривать пространство непрерывных функций с нормой _H=, H=[a,b],

а сеточную функцию определять как y_h(x)=u_h(x), x w_h

2. Норма 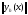_Hh=

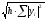
удовлетворяют условию (2), если за Н принять пространство непрерывных функций с нормой 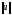_H=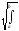u²(x)dx, H=C[a,b] ,

а сеточную функцию определять в виде y_h=u_h(x), x w_h.