
- •1.1. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса (вычислительная сложность, выбор ведущего элемента).
- •1.2. Понятие об одношаговых и многошаговых методах. Метод Эйлера решения задачи Коши для системы оду первого порядка.
- •2.1. Lu представление матрицы. Обращение матриц и вычисление определителя.
- •2.2. Локальная и глобальная ошибка одношагового метода решения задачи Коши. Задача для погрешности метода, устойчивость и сходимость.
- •3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм
- •3.2. Методы Рунге-Кутта. Схема метода четвертого порядка.
- •Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лау
- •Многошаговые методы. Явные и неявные методы. Метод Адамса
- •5.1. Понятие устойчивости численных методов для жестких систем. Метод Гира.
- •5.2. Итерационные методы решения систем лау. Метод простой итерации. Условия сходимости и критерий остановки итераций.
- •6.2. Разностная аппроксимация дифференциальных операторов. Сеточный шаблон. Явные и неявные схемы для нестационарных задач математической физики.
- •7.1. Прямые методы вычисления собственных значений. Преобразования подобия. Метод Данилевского.
- •7.2. Порядок аппроксимации разностной схемы. Оценка порядка аппроксимации разностной схемы с весами для нестационарного уравнения теплопроводности.
- •8.1. Оптимальное значение итерационного параметра. Метод минимальных невязок.
- •8.2. Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.
- •9.1. Итерационные методы решения проблемы собственных значений. Степенной метод.
- •9.2. Спектральный метод исследования устойчивости разностных схем для уравнений с постоянными коэффициентами.
- •10.1. Итерационные методы решения нелинейных уравнений. Метод Ньютона.
- •10.2. Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
- •21.1. Спектр собственных значений разностного оператора второй производной.
- •21.2. Разностные аналоги формул Грина и теоремы вложения норм сеточных функций.
-
Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лау
Пусть правая часть системы возмущена
– задана с абсолютной погрешностью
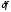 .
Тогда фактически вместо
.
Тогда фактически вместо
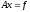 мы решаем возмущенную задачу
мы решаем возмущенную задачу
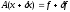 (1)
(1)
где
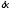 – абсолютная погрешность решения,
ассоциированная с возмущением правой
части. Погрешность
– абсолютная погрешность решения,
ассоциированная с возмущением правой
части. Погрешность
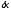 является решением следующей задачи:
является решением следующей задачи:
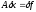 (2)
(2)
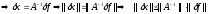 (3)
- норма абс. вел-ны погрешности
(3)
- норма абс. вел-ны погрешности
Последнее
неравенство (3) выражает устойчивость
решения по правой части, что эквивалентно
требованию ограниченности
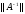 .
Из постановки задачи имеем
.
Из постановки задачи имеем
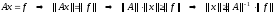 .
(4)
.
(4)
Из неравенств (3) и (4) следует оценка относительной погрешности возмущенной задачи:
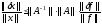 (5)
(5)
Согласно
(5) погрешность возмущенной задачи
пропорционально возрастает с ростом
возмущений правой части, причем
коэффициент пропорциональности
определяется произведением норм матриц
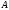 и
и
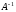 .
Число
.
Число
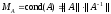 ,
(6)
,
(6)
характеризующее
зависимость относительной погрешности
решения СЛАУ от величины относительного
возмущения правой части, называется
числом обусловленности
матрицы. Если
число обусловленности матрицы велико,
то говорят, что данная матрица плохо
обусловлена. Если число обусловленности
близко к единице, то матрица считается
хорошо обусловленной. Обычно
для оценки числа обусловленности
используется спектральная норма матриц
(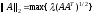 ,
сингулярные числа матрицы вычисляются
как корень из совпадающих собственных
значений матриц
,
сингулярные числа матрицы вычисляются
как корень из совпадающих собственных
значений матриц
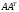 ),
которая является подчиненной для
евклидовой векторной нормы. Для
симметричных матриц
число обусловленности определяется
отношением модулей наибольшего и
наименьшего собственного значения
матрицы.
),
которая является подчиненной для
евклидовой векторной нормы. Для
симметричных матриц
число обусловленности определяется
отношением модулей наибольшего и
наименьшего собственного значения
матрицы.
Для плохо обусловленных матриц малая
ошибка входных данных приводит к
существенному изменению решения;
аналогичным образом и для погрешности
промежуточных вычислений. Так, например,
в процессе приведения матрицы системы
к треугольному виду выполняется ряд
преобразований ее коэффициентов. В
итоге, на этапе обратного хода метода
Гаусса решается задача с возмущенными
коэффициентами матрицы и полная оценка
относительной погрешности должна
исходить из следующей возмущенной
задачи:
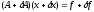 ,
(7)
,
(7)
Если матрица возмущенной задачи (7) не
вырожденная, то возмущения коэффициентов
матрицы могут быть соотнесены с
возмущениями правой части и вместо
задачи (7) достаточно
рассмотреть задачу
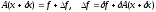 (8)
(8)
для
которой имеет место оценка (5). На
практике величина
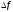 может быть вычислена на основе полученного
приближенного решения задачи
может быть вычислена на основе полученного
приближенного решения задачи
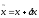 :
:
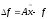 (9)
(9)
Вектор
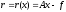 принято называть невязкой
решения СЛАУ. Норма данного
вектора на практике служит количественной
мерой возмущения правой части задачи
и используется для оценки погрешности
приближенного решения.
принято называть невязкой
решения СЛАУ. Норма данного
вектора на практике служит количественной
мерой возмущения правой части задачи
и используется для оценки погрешности
приближенного решения.
Оценки числа обусловленности матриц требуют вычисления обратной матрицы или, по крайней мере, оценки максимального и минимального собственных значений в случае симметричных матриц. В силу этого практическая оценка фактической точности приближенного решения системы ЛАУ согласно неравенству (5) представляет собой сложную задачу. Тем не менее, для ряда практически значимых случаев оценка (5) представляется полезной в плане контроля точности вычислений.
