1.2. Понятие об одношаговых и многошаговых методах. Метод Эйлера решения задачи Коши для системы оду первого порядка.

Метод Эйлера: Рассмотрим задачу Коши для уравнения вида (1)

Представим решения отрезком степенного ряда, которое даёт точное решение (1):

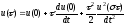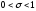, . (2)

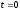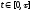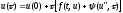Мы знаем решение в точке , а правая часть уравнения позволяет вычислить производную решения в данной точке. В итоге, полагая ограниченность второй производной решения на отрезке , имеем (3)

где, , .

Заметим, что (3) также дает точное решения в точке 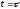. Но мы не можем использовать его в практических расчетах, т.к. для этого требуется значение второй производной от решения, содержащейся в члене (не знаем о ней) и не знаем точное положение точки, в которой требуется вычислить данную производную. Так что пренебрегаем данным членом, учитывая, что при ограниченной второй производной величина данного члена стремиться к нулю при 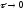=> приходим к схеме Эйлера, позволяющей найти приближенно шаг за шагом решение задачи Коши 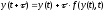(4)

Используя формулу Эйлера (4) мы можем последовательно найти приближенно решение задачи Коши на некотором множестве точек, соответствующих значениям независимой переменной 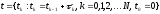(5) – сетка.

Отдельные точки сетки называют узлами. Шагом сетки называется расстояние между соседними узлами 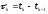. Если все шаги сетки одинаковы, то сетка называется равномерной (однородной). Множество значений функции, определяемых в узлах сетки, называется сеточной функцией. Сеточные функции не обязательно являются результатом приближенного (численного) решения дифференциальной задачи. Точное решение задачи, например, если оно может быть выражено в виде элементарных или специальных функции, также может быть представлено в виде набора значений данной функции в узлах сетки, т.е. в виде сеточной функции.

Сеточные функции могут рассматриваться как некоторые векторы конечной размерности. Для сравнения сеточных функций и оценок их близости естественно воспользоваться аппаратом функционального анализа, рассматривая их как элементы некоторого линейного векторного пространства с определенной нормой.

ТЕОРЕМА 1. Метод Эйлера (4) имеет первый порядок аппроксимации на решении задачи Коши (1) с функцией 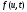, удовлетворяющей условиям

,

и для глобальной погрешности приближенного решения справедлива оценка

Если приближенное решение в новом узле сетки вычисляется с использованием информации только в одном предыдущем узле сетки, то методы такого типа принято называть одношаговыми.

Многошаговые методы, если приближенное решение в произвольном 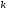-том узле сетки вычисляется с использованием значений приближенного решения в предыдущих узлах сетки.

2.1. Lu представление матрицы. Обращение матриц и вычисление определителя.

При приведении матрицы СЛАУ к треугольному виду (вычислительная сложность прямого хода метода Гаусса на порядок превосходит вычислительные затраты на обратный ход) целесообразно оптимизировать метод. Данная модификация метода Гаусса получила название 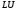- факторизация. Само название указывает на то, что суть данного метода состоит в разложении матрицы на два сомножителя и – соответственно нижнюю и верхнюю треугольные матрицы.

Основной теоретический результат, касающийся существования и единственности представления матрицы вида заключается в следующем

Теорема. Если 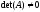, то существует матрица перестановок 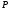такая, что имеет место разложение (1), где 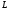– нижняя треугольная с отличными от нуля диагональными элементами, - верхняя треугольная с единичной главной диаг-ю.

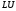=>-факторизация может использоваться для произвольной невырожденной матрицы.

Алгоритм вычисления матриц и во многом повторяет прямой ход метода Гаусса. В частности, из равенства 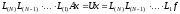следует

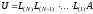(2)

Умножим равенство (2) на произведение матриц 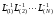, в результате имеем:

.

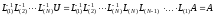Из полученного равенства следует (3)

Относительно элементарных треугольных матриц 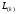известно, что обратные им матрицы также являются элементарными треугольными, причем:

Как и в методе Гаусса при использовании алгоритма - факторизации на этапе формирования матриц 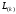может оказаться => стратегии выбора ведущего элемента путем перестановки строк (столбцов) матрицы.

Вычислительная сложность алгоритма 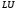- факторизации 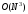, т.е. по порядку величины не превосходит вычислительные затраты в методе Гаусса.

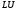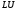Алгоритм разложения полезен в тех случаях, когда требуется решить несколько систем ЛАУ с одной и той же матрицей и разными правыми частями. После того как разложение матрицы получено, задача решения системы линейных алгебраических уравнений сводится к последовательному решению двух систем с матрицами треугольного вида: . Таким образом, однократное выполнение разложения позволяет на порядок сократить вычислительные затраты при серийных расчетах (многократных решениях систем ЛАУ с одинаковой матрицей).

LU-разложение используется для решения систем линейных уравнений и для обращения матриц. Этот метод является одной из разновидностей метода Гаусса.