
- •1.1. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса (вычислительная сложность, выбор ведущего элемента).
- •1.2. Понятие об одношаговых и многошаговых методах. Метод Эйлера решения задачи Коши для системы оду первого порядка.
- •2.1. Lu представление матрицы. Обращение матриц и вычисление определителя.
- •2.2. Локальная и глобальная ошибка одношагового метода решения задачи Коши. Задача для погрешности метода, устойчивость и сходимость.
- •3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм
- •3.2. Методы Рунге-Кутта. Схема метода четвертого порядка.
- •Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лау
- •Многошаговые методы. Явные и неявные методы. Метод Адамса
- •5.1. Понятие устойчивости численных методов для жестких систем. Метод Гира.
- •5.2. Итерационные методы решения систем лау. Метод простой итерации. Условия сходимости и критерий остановки итераций.
- •6.2. Разностная аппроксимация дифференциальных операторов. Сеточный шаблон. Явные и неявные схемы для нестационарных задач математической физики.
- •7.1. Прямые методы вычисления собственных значений. Преобразования подобия. Метод Данилевского.
- •7.2. Порядок аппроксимации разностной схемы. Оценка порядка аппроксимации разностной схемы с весами для нестационарного уравнения теплопроводности.
- •8.1. Оптимальное значение итерационного параметра. Метод минимальных невязок.
- •8.2. Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.
- •9.1. Итерационные методы решения проблемы собственных значений. Степенной метод.
- •9.2. Спектральный метод исследования устойчивости разностных схем для уравнений с постоянными коэффициентами.
- •10.1. Итерационные методы решения нелинейных уравнений. Метод Ньютона.
- •10.2. Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
- •21.1. Спектр собственных значений разностного оператора второй производной.
- •21.2. Разностные аналоги формул Грина и теоремы вложения норм сеточных функций.
10.1. Итерационные методы решения нелинейных уравнений. Метод Ньютона.
В отличие от систем линейных
алгебраических уравнений, для решения
которых могут применяться как прямые
(или точные),
так и итерационные
(или приближенные)
методы, решение систем нелинейных
уравнений можно получить только
приближенными, итерационными методами.
Они позволяют получать последовательность
приближений
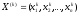
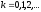 .
Если итерационный процесс сходится, то
граничное значение
.
Если итерационный процесс сходится, то
граничное значение
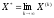 является решением данной системы
уравнений.
является решением данной системы
уравнений.
Рассмотрим нелинейную систему уравнений
(1)
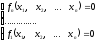
Она может быть также
представлена в матричном виде:
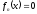 (1’), где
(1’), где
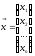
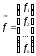
Её решением называется
такое значение
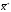 ,
для котрого
,
для котрого
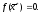
Если для посл. xn,
сходящейся к х*,
верна формула:
![]()
(k – положит-е действ-е число), то k - скорость сходимости данной последовательности.
Итерационные методы решения систем нелинейных уравнений: метод простых итераций, преобразование Эйткена, метод Ньютона, метод градиентного спуска, метод Пикара
Метод Ньютона
Основная идея метода Ньютона состоит в выделении из уравнений линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем.
Рассмотрим систему уравнений: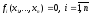
в предположении, что
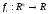 – непрерывно-дифференцируемые функции.
– непрерывно-дифференцируемые функции.
Полагая
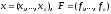 ,
перейдём к векторной записи
,
перейдём к векторной записи
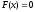 (2)
(2)
Опишем общий шаг метода.
Пусть уже получено приближение
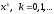 Разложим функцию
Разложим функцию
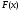 в ряд Тейлора, оставив только два первых
члена в силу малости отклонения
приближения
в ряд Тейлора, оставив только два первых
члена в силу малости отклонения
приближения
 от корня:
от корня:
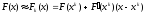 ,
,
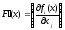 –
матрица Якоби для
–
матрица Якоби для
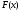 .
.
Очередное приближение
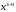 определяется как решение линейной
системы
определяется как решение линейной
системы
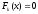 ,
т.е.
,
т.е.
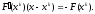
Если матрица Якоби
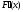 не вырождена, то решение системы линейной
системы можно записать в явном виде,
что приводит к стандартной
формуле метода Ньютона
не вырождена, то решение системы линейной
системы можно записать в явном виде,
что приводит к стандартной
формуле метода Ньютона
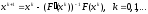 (3)
(3)
Таким образом, в основе
метода Ньютона лежит идея линеаризации
вектор-функции
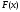 в окрестности каждого приближения (на
каждой итерации), что позволяет свести
решение системы (2) к последовательному
решению линейных систем.
в окрестности каждого приближения (на
каждой итерации), что позволяет свести
решение системы (2) к последовательному
решению линейных систем.
Через уже известное
приближение
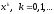 к корню
к корню
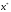 можно записать, что
можно записать, что
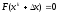 ,
где
,
где
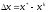 .
Тогда после линеаризации получим систему
уравнений, линейную относительно
.
Тогда после линеаризации получим систему
уравнений, линейную относительно
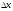 .
Таким образом, на каждом шаге мы будем
находить приращения
.
Таким образом, на каждом шаге мы будем
находить приращения
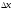 ,
и новое приближение к решению по формулам:
,
и новое приближение к решению по формулам:
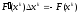 – система линейных уравнений.
– система линейных уравнений.
Точное условие сходимости метода Ньютона имеет достаточно сложный вид. Но очевидный результат: в достаточно малой окрестности корня итерации сходятся, если матрица Якоби невырожденная, причём сходимость квадратичная.
Пусть в
 выбрана нек-я векторная
выбрана нек-я векторная
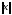 и согласованная с ней матричная
и согласованная с ней матричная
 .
.
Теорема (о сходимости). Пусть
1) вектор-функция
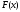 определена и непрерывно-дифференцируема
в области
определена и непрерывно-дифференцируема
в области
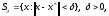 где
где
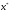 – решение уравнения (2),
– решение уравнения (2),
2) для всех
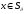 существует обратная матрица
существует обратная матрица
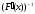 ,
причём
,
причём
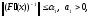
3) для всех
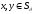
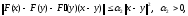
4)
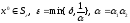
Тогда метод Ньютона (3)
1)
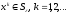
2)
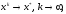
3)
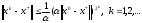
Замечание.
Оценка погрешности метода Ньютона:
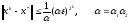
10.2. Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
Решение разностной задачи
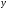 сходится к решению дифференциальной
задачи
сходится к решению дифференциальной
задачи
 ,если
при
,если
при
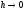
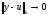 ,
где
,
где
 некоторая норма в пространстве сеточных
функций.
некоторая норма в пространстве сеточных
функций.
Разностная
схема имеет
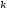 -й
порядок точности по шагу h
(или h и
-й
порядок точности по шагу h
(или h и ),
если для погрешности приближенного
решения
),
если для погрешности приближенного
решения
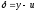 при любых достаточно малых шагах сетки
выполняется оценка
при любых достаточно малых шагах сетки
выполняется оценка
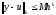 ,
(или
,
(или
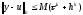 ).
Порядок точности разностных схем
относительно шагов сетки по пространственной
и временной переменной, вообще говоря,
не обязательно совпадает.
).
Порядок точности разностных схем
относительно шагов сетки по пространственной
и временной переменной, вообще говоря,
не обязательно совпадает.
Разность между дискретными и непрерывными производными принято называть погрешностью аппроксимации или ошибкой дискретизации дифференциального оператора на данной функции. Погрешность аппроксимации дифференциальных операторов может быть выражена путем разложения дифференцируемой функции в степенной ряд в окрестности фиксированного узла сетки (если возможно). Погрешность аппроксимации дискретной модели складывается из погрешностей аппроксимации каждого из ее элементов (погрешности аппроксимации производных, граничных условий, коэффициентов, функций и т.п.).
Разностная схема аппроксимирует дифференциальную задачу, если погрешность аппроксимации данной разностной схемы на решении дифференциальной задачи стремиться к нулю при шагах сетки, стремящихся к нулю.
Следует подчеркнуть отличие понятий погрешности приближенного решения и погрешности аппроксимации задачи. Погрешность решения определяется разностью между точным решением и некоторым его приближением. Погрешность аппроксимации дискретной задачи выражает невязку, которая возникают при подстановке точного решения в уравнения дискретной задачи, характеризует величину возмущений, связанных с переходом от дифференциальной модели к дискретной.
!!Устойчивость дискретной модели не следует из устойчивости дифференциальной задачи, которую данная дискретная модель аппроксимирует.
Разностная схема называется устойчивой, если ее решение непрерывно зависит от входных данных, т. е. малому изменению входных данных соответствует малое изменение решения.
Устойчивость характеризует чувствительность разностной схемы к различного рода погрешностям, она является внутренним свойством разностной задачи, и это свойство не связывается непосредственно с исходной дифференциальной задачей (в отличие от сходимости).
Устойчивость бывает условной и безусловной в зависимости от того, накладываются ли ограничения на соотношения между шагами по разным переменным.
Если решение исходной дифференциальной задачи существует, а разностная схема устойчива и аппроксимирует задачу, то разностное решение сходится к точному.
Для доказательства устойчивости
дискретной модели
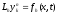 достаточно
доказать, что приближенное решение
удовлетворяет неравенству
достаточно
доказать, что приближенное решение
удовлетворяет неравенству
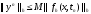 ,
,
M – постоянная, не зависящая от шагов сетки. Это неравенство фактически означает непрерывную зависимость приближенного решения от правой части.
Произвольное частное решение дискретной
задачи ищется в виде
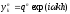
Подстановка
такой сеточной функции в разностное
уравнение позволяет определить, при
каких значениях
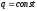 данная сеточная функция удовлетворяет
разностному уравнению.
данная сеточная функция удовлетворяет
разностному уравнению.
- Если
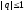 для произвольных действительных
для произвольных действительных
 ,
данное решение будет устойчивым.
,
данное решение будет устойчивым.
- Если же,
напротив, для некоторого значения
 мы получим
мы получим
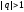 ,
то такое частное решение будет
неограниченно возрастать при
,
то такое частное решение будет
неограниченно возрастать при
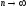 ,
т.е. является неустойчивым.
,
т.е. является неустойчивым.
