
- •1.1. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса (вычислительная сложность, выбор ведущего элемента).
- •1.2. Понятие об одношаговых и многошаговых методах. Метод Эйлера решения задачи Коши для системы оду первого порядка.
- •2.1. Lu представление матрицы. Обращение матриц и вычисление определителя.
- •2.2. Локальная и глобальная ошибка одношагового метода решения задачи Коши. Задача для погрешности метода, устойчивость и сходимость.
- •3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм
- •3.2. Методы Рунге-Кутта. Схема метода четвертого порядка.
- •Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лау
- •Многошаговые методы. Явные и неявные методы. Метод Адамса
- •5.1. Понятие устойчивости численных методов для жестких систем. Метод Гира.
- •5.2. Итерационные методы решения систем лау. Метод простой итерации. Условия сходимости и критерий остановки итераций.
- •6.2. Разностная аппроксимация дифференциальных операторов. Сеточный шаблон. Явные и неявные схемы для нестационарных задач математической физики.
- •7.1. Прямые методы вычисления собственных значений. Преобразования подобия. Метод Данилевского.
- •7.2. Порядок аппроксимации разностной схемы. Оценка порядка аппроксимации разностной схемы с весами для нестационарного уравнения теплопроводности.
- •8.1. Оптимальное значение итерационного параметра. Метод минимальных невязок.
- •8.2. Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.
- •9.1. Итерационные методы решения проблемы собственных значений. Степенной метод.
- •9.2. Спектральный метод исследования устойчивости разностных схем для уравнений с постоянными коэффициентами.
- •10.1. Итерационные методы решения нелинейных уравнений. Метод Ньютона.
- •10.2. Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
- •21.1. Спектр собственных значений разностного оператора второй производной.
- •21.2. Разностные аналоги формул Грина и теоремы вложения норм сеточных функций.
7.1. Прямые методы вычисления собственных значений. Преобразования подобия. Метод Данилевского.
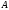 - квадратная невырожденная матрица.
Число
- квадратная невырожденная матрица.
Число
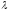 -собственное значение
-собственное значение
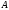 ,
если существует такой ненулевой вектор
,
если существует такой ненулевой вектор
 ,
удовлетворяющий равенству
,
удовлетворяющий равенству
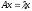 (1). Сов-ть всех собственных значений -
спектр. Вектор
(1). Сов-ть всех собственных значений -
спектр. Вектор
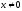 ,
удовлетворяющий (1) - собственный вектор
,
удовлетворяющий (1) - собственный вектор
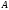 . Уравнение
(1) имеет нетривиальные решения
. Уравнение
(1) имеет нетривиальные решения 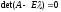 (2)
(2)
Функция
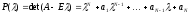 - характеристический многочлен
матрицы. Множество его корней совпадает
со спектром.
- характеристический многочлен
матрицы. Множество его корней совпадает
со спектром.
Прямой метод вычисления собственных значений:
В прямом методе получают хар-е ур-е в аналитическом виде или определяют алгоритм выч-я коэфф-в уравнения, потом решают это ур-е одним из численных методов.
det(A-λE)
= D(λ ) может быть представлен в виде
D(λ ) =
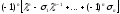
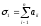 - сумма всех диагональных миноров первого
порядка матрицы А.
- сумма всех диагональных миноров первого
порядка матрицы А.
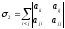 - cумма всех диагональных
миноров второго порядка.
- cумма всех диагональных
миноров второго порядка.
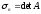 .
Вычислив
.
Вычислив
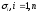 ,
находим корни полинома одним из численных
методов.
,
находим корни полинома одним из численных
методов.
Наиболее эффективный подход к проблеме собственных значений основан на использовании преобразований подобия, позволяющих привести исходную матрицу к треугольному, диагональному или блочно-диагональному виду. Поскольку преобразование подобия не меняет спектр матрицы, то применение такого рода преобразований во многих случаях приводит к решению полной проблемы собственных значений. Наиболее эффективны преобразования подобия в случае симметричных матриц.
Однако во многих случаях достаточно предположить, что среди собственных значений матрицы отсутствуют кратные. В этом случае существует преобразование подобие, приводящее матрицу к диагональному виду.
Способ
построения преобразования подобия:
исп-е элем-х матриц плоских вращений
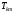 :
:
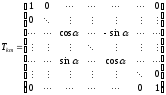 (3)
(3)
Матрица
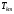 (для определенности пусть
(для определенности пусть
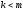 )
отличается от единичной матрицы только
элементами
)
отличается от единичной матрицы только
элементами
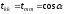 и
и
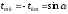 .
.
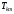 - ортогональные =>
- ортогональные =>
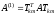 -
преобразование плоских вращений,
является преобразованием подобия. При
умножении матрицы слева (справа) на
-
преобразование плоских вращений,
является преобразованием подобия. При
умножении матрицы слева (справа) на
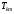 новая матрица отличается от исходной
лишь эл-ми строк с номерами
новая матрица отличается от исходной
лишь эл-ми строк с номерами
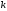 и
и
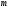 (столбцами). Полагая
(столбцами). Полагая
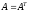 ,
рассмотрим произведения:
,
рассмотрим произведения:
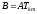 :
:
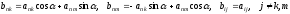 ,
,
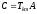 :
:
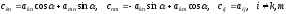 .
.
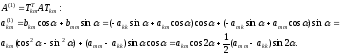
Определим
угол вращения таким образом, чтобы
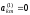 .
.
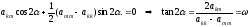 .
.
Используя тригонометрические тождества, имеем:
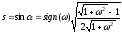 ,
,
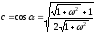 . (4)
. (4)
При
выбранном угле поворота в результате
преобразования
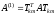 уменьшается общая сумма квадратов
недиагональных элементов результирующей
матрицы. Многократное применение такого
рода преобразования с матрицами вращения
уменьшается общая сумма квадратов
недиагональных элементов результирующей
матрицы. Многократное применение такого
рода преобразования с матрицами вращения
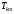 :
на текущем шаге
:
на текущем шаге
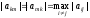 ,
приводит к сходимости последовательности
матриц
,
приводит к сходимости последовательности
матриц
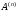 ,
,
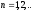 к
матрице диагонального вида, при этом
на диагонали новой матрицы будут
находиться приближенные значения
собственных чисел исходной матрицы
к
матрице диагонального вида, при этом
на диагонали новой матрицы будут
находиться приближенные значения
собственных чисел исходной матрицы
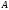 .
.
Метод Данилевского: Большая погрешность, но большая скорость получения результата.
Метод основан
на известном факте из линейной алгебры
о том, что преобразование подобия
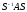 не
меняет характеристического многочлена
матрицы
не
меняет характеристического многочлена
матрицы
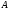 ,
т.к.
,
т.к.
![]() .
.
(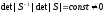 =>
при записи характер-го уравнения на
него сокращаем).
=>
при записи характер-го уравнения на
него сокращаем).
Приводим
матрицу 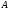 с помощью преобразования подобия
с помощью преобразования подобия
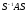 к
так называемой канонической форме
Фробениуса:
к
так называемой канонической форме
Фробениуса:
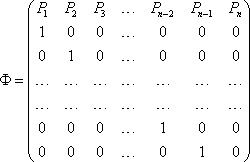
Для
матрицы
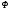 характеристический
многочлен может быть легко записан,
если последовательно разлагать
определитель
характеристический
многочлен может быть легко записан,
если последовательно разлагать
определитель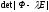 по элементам первого столбца =>
по элементам первого столбца =>![]()
=> элементы
1-й строки
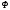 являются
коэффициентами её собственного многочлена
=> собственного многочлена матрицы
являются
коэффициентами её собственного многочлена
=> собственного многочлена матрицы
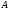 .
.
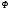 и
и
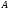 связаны
между собой:
связаны
между собой:
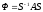
Решив
полученное уравнение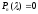 ,
находим собственные значения матрицы
,
находим собственные значения матрицы
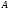 .
Далее, неособенная матрица
.
Далее, неособенная матрица
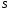 ,
полученная в методе Данилевского,
используется при нахождении собственных
векторов матрицы
,
полученная в методе Данилевского,
используется при нахождении собственных
векторов матрицы
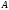 .
.
Построение матрицы
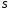 в
методе Данилевского осуществляется
последовательно с помощью
в
методе Данилевского осуществляется
последовательно с помощью
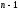 преобразований
подобия, которые переводят строки
матрицы
преобразований
подобия, которые переводят строки
матрицы
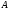 ,
начиная с последней, в соответствующие
строки матрицы
,
начиная с последней, в соответствующие
строки матрицы
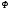 .
.
