1.1. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса (вычислительная сложность, выбор ведущего элемента).

Решение СЛАУ для заданного вектора 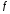и квадратной матрицы 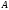размерности 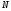состоит в поиске вектора , удовлетворяющего равенству 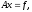(1) Данная задача для произвольного вектора 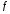имеет единственное решение при условии, что матрица 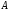не вырожденная (не имеет линейно зависимых строк).

Вычислительная сложность нахождения определителя матрицы имеет порядок 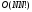+ нахождение определителя (за исключением det(A)=0), как вычислительная задача не представляет интереса в силу приближенности компьютерных вычислений.

Наряду с системой уравнений (1) рассмотрим возмущенную задачу 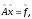(2) где 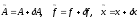. 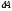, 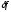– возмущения элементов матрицы и вектора правой части задачи, а 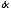– разность между решениями возмущенной и исходной задачи. Задача считается устойчивой, если ее решение непрерывно зависит от возмущений входных данных. 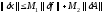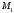Условие устойчивости может быть сформулировано в виде оценки возмущения решения задачи от возмущения входных данных: , где , и 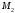некоторые постоянные, зависящие от свойств матрицы .

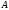Метод Гаусса

Большинство прямых методов решения СЛАУ в той или иной мере наследуют идею алгоритма последовательного исключения неизвестных – метода Гаусса. Если матрица задачи, например, является верхней треугольной, то произвольное k-ое уравнение системы имеет вид 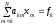, , 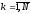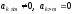(3)

Последнее уравнение системы содержит всего лишь одно неизвестное 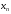, и его значение вычисляется первым: 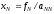(4)

Остальные неизвестные вычисляются последовательно по явным формулам

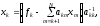
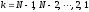(5)

Аналогичный алгоритм м.б. построен для задачи с нижней треугольной матрицей.

Суть метода Гаусса состоит в приведении матрицы задачи к верхнему (нижнему) треугольному виду. Для этих целей используются тождественные преобразования системы. В частности, решение задачи не меняется при замене произвольной строки системы на линейную комбинацию данной строки и произвольного числа других строк системы. Используя такого рода преобразования, можно последовательно, столбец за столбцом, исключить переменные, находящиеся ниже главной диагонали системы ЛАУ. Элементарный шаг такого преобразования можно выразить с помощью операции умножения л. и пр. части системы на элементарную нижнюю треугольную матрицу вида:

(6)

Матрицы 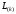отличаются от единичной тем, что -ый столбец данной матрицы, начиная с элемента 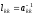, и ниже 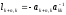, , 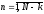формируется специальным образом (6) из соответствующих значений элементов преобразуемой матрицы. В результате умножения 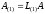(7) преобразованная матрица 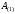будет иметь нулевые значения элементов первого столбца ниже главной диагонали: 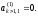Далее, на основе элементов матриц 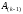, 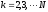последовательно формируются матрицы 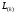и находятся 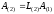, , 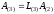… 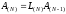(8)

Нетрудно убедиться, что после выполнения описанных действий матрица 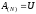будет верхней треугольной матрицей с единицами на главной диагонали.

Таким образом, метод последовательного исключения Гаусса состоит в преобразовании исходной системы уравнений путем умножения ее на элементарные треугольные матрицы, в результате чего исходная система преобразуется в эквивалентную систему с верхней треугольной матрицей 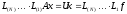(9)

Решение полученной системы уравнений находится с помощью алгоритма (4), (5).

Процедуру (7) – (9) принято называть прямым ходом метода Гаусса, а (4), (5) – соответственно обратный ход.

Оценим вычислительные затраты прямого и обратного хода метода Гаусса.

Одна операция умножения 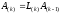имеет выч-ю сложность порядка .

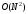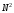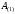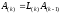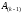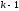В самом деле, каждый элемент матричного произведения находится как скалярное произведение двух векторов, причем вектор первого из сомножителей имеет не более двух ненулевых элементов (строка). В результате каждый из элементов матрицы вычисляется не более чем за два умножения и одно сложение. Несложно заметить, что в процессе умножения элементы матрицы , расположенные выше -ой строки и левее 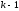-го столбца, остаются неизменными: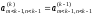. По этой причине вычислительная сложность умножения матриц 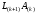уменьшается с ростом 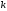и не превосходит 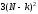. Таким образом, вычислительные затраты на реализацию прямого хода метода Гаусса составляют 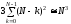операций умножения и сложения. Формирование матриц 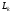требует приблизительно 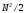операций. С учетом вышесказанного для матриц достаточно большой размерности 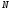можно оценить выч-ю сложность прямого хода метода Гаусса величиной .

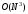Для обратного хода метода Гаусса из выражения (5) легко подсчитать, что для вычисления 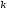-ой компоненты решения требуется 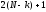операций. Суммирование вычислительных затрат для определения всех 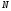неизвестных дает приблизительно 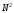операций, что на порядок меньше вычислительной сложности прямого метода Гаусса.

Метод Гаусса является самым универсальным в своем классе и может быть использован для решения произвольных СЛАУ с невырожденной матрицей. Тем не менее, источником проблем являются нулевые (близкие к нулю) значения диагональных элементов, присутствующие в матрице изначально, либо появляющиеся в процессе исключения неизвестных. Как видно из выражения (6), при формировании матриц 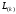выполняется деление на 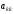, что в случае 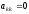приводит к потере корректности алгоритма. Для устранения этих проблем используется алгоритмы перестановок столбцов (строк) матрицы.

Метод Гаусса с выбором ведущего элемента

При перестановке строк СЛАУ решение задачи не изменяться. Данное свойство лежит в основе алгоритмов упорядочения строк матрицы.

Стратегия частичного упорядочения состоит в следующем. Прежде чем приступить к формированию матрицы 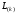производится перестановка строк матрицы 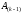с номерам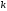и и 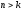, причем значение определяется из условия 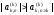. Таким образом, на позиции ведущего элемента 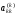после перестановки строк оказывается максимальный по модулю из элементов 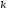-го столбца, расположенных ниже главной диагонали. Использование данных перестановок позволяет избежать деления на нуль при формировании матриц 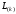+ часто предотвращает деление на числа близкие к нуль.

Алгоритмически перестановку строк матрицы можно реализовать путем умножения матрицы перестановок на преобразуемую матрицу. Матрицей перестановок называется матрица, в каждой строке и каждом столбце которой содержится только один ненулевой элемент, равный единице, а остальные элементы равны нулю. Частным случает матрицы перестановок является единичная матрица. Элементарной матрицей перестановки называется матрица 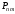, полученная из единичной матрицы путем перестановки в ней строк с номерами и . 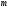Умножение матрицы 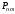на матрицу 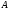приводит к перестановке в последней -ой и 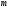-ой строк.

Матрицы перестановок обладают рядом замечательных свойств.

- Матрица перестановок является унитарной матрицей: .

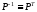- Произведение любого числа матриц перестановок является матрицей перестановок.

- Произвольную перестановку строк матрицы можно осуществить с помощью матрицы перестановок, полученной из произведения элементарных матриц перестановок.

Алгоритм частичного упорядочения с выбором главного элемента по столбцам фактически состоит в определении позиции главного элемента и построении элементарной матрицы перестановок.

Пусть, например, при исключении неизвестных в СЛАУ с матрицей 5x5 после двух шагов исключения неизвестных имеем, что ведущий элемент 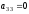, максимальный элемент третьего столбца находится в четвертой строке:

. Тогда ,

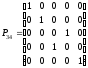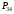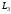Использование позволяет предотвратить деление на нуль. Далее, формируется матрица , вычисляется 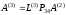и выполняется следующий шаг исключения.

Замечание 1. Кроме рассмотренного алгоритма частичного упорядочения с выбором главного элемента по столбцам существуют аналогичные варианты упорядочения по строкам, а также по строкам и столбцам одновременно.

Замечание 2. Надежность алгоритма частичного упорядочения существенно повышается, если матрица системы ЛАУ масштабирована таким образом, что максимальные значения модулей элементов в каждой строке и каждом столбце имеют одинаковый порядок. Если матрица не отвечает требованиям масштабирования полезно, по крайней мере, предварительно выполнить нормировку строк, нарушающих баланс матрицы.

Замечание 3. Среди немногочисленных случаев, когда частичное упорядочение оказывается излишним, можно отметить диагонально-доминирующие и симметричные положительно-определенные матрицы.