
- •1.1. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса (вычислительная сложность, выбор ведущего элемента).
- •1.2. Понятие об одношаговых и многошаговых методах. Метод Эйлера решения задачи Коши для системы оду первого порядка.
- •2.1. Lu представление матрицы. Обращение матриц и вычисление определителя.
- •2.2. Локальная и глобальная ошибка одношагового метода решения задачи Коши. Задача для погрешности метода, устойчивость и сходимость.
- •3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм
- •3.2. Методы Рунге-Кутта. Схема метода четвертого порядка.
- •Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лау
- •Многошаговые методы. Явные и неявные методы. Метод Адамса
- •5.1. Понятие устойчивости численных методов для жестких систем. Метод Гира.
- •5.2. Итерационные методы решения систем лау. Метод простой итерации. Условия сходимости и критерий остановки итераций.
- •6.2. Разностная аппроксимация дифференциальных операторов. Сеточный шаблон. Явные и неявные схемы для нестационарных задач математической физики.
- •7.1. Прямые методы вычисления собственных значений. Преобразования подобия. Метод Данилевского.
- •7.2. Порядок аппроксимации разностной схемы. Оценка порядка аппроксимации разностной схемы с весами для нестационарного уравнения теплопроводности.
- •8.1. Оптимальное значение итерационного параметра. Метод минимальных невязок.
- •8.2. Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.
- •9.1. Итерационные методы решения проблемы собственных значений. Степенной метод.
- •9.2. Спектральный метод исследования устойчивости разностных схем для уравнений с постоянными коэффициентами.
- •10.1. Итерационные методы решения нелинейных уравнений. Метод Ньютона.
- •10.2. Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
- •21.1. Спектр собственных значений разностного оператора второй производной.
- •21.2. Разностные аналоги формул Грина и теоремы вложения норм сеточных функций.
21.2. Разностные аналоги формул Грина и теоремы вложения норм сеточных функций.
Основной вопрос теории численных методов
состоит в оценке точности приближенного
решения задачи. Для разностных методов
погрешность приближенного решения
зависит от шага сетки h.
Под сходимостью разностных схем понимают
сходимость приближенного решения
разностных уравнений к решению исходной
дифференциальной задачи при
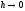 .
В случае неравномерных сеток сходимость
разностного решения определяется при
стремлении к нулю максимального шага
сетки. Будем говорить, что скорость
сходимости разностной схемы имеет
порядок p,
если разность точного и приближенного
решений (погрешность приближенного
решения) стремиться к нулю как
.
В случае неравномерных сеток сходимость
разностного решения определяется при
стремлении к нулю максимального шага
сетки. Будем говорить, что скорость
сходимости разностной схемы имеет
порядок p,
если разность точного и приближенного
решений (погрешность приближенного
решения) стремиться к нулю как
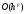 .
.
При исследовании вопросов сходимости разностных методов естественно рассматривать сеточные функции точного и приближенного решений как элементы некоторого конечномерного векторного пространства, а оценки погрешности метода выражать в нормах рассматриваемого векторного пространства.
Итак, рассмотрим пространство сеточных
функций
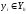 ,
определенных на сетке
,
определенных на сетке
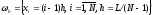
Наиболее
широкое распространение в теории
разностных схем получили следующие
нормы сеточных функций
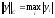 (1) и
(1) и
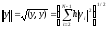 (2)
(2)
Несложно заметить, что в пространстве сеточных функций, равных нулю в граничных точках сетки, нормы (1) и (2) связаны следующим соотношением
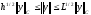 (3)
(3)
Утверждение
1. Для произвольных сеточных
функций
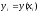 ,
,
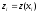 ,
,
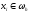 выполняется разностные аналоги формулы
интегрирования по частям:
выполняется разностные аналоги формулы
интегрирования по частям:
 ,
(4) и
,
(4) и
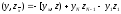 (5), где
(5), где
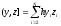 ,
,
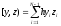 ,
,
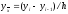 ,
,
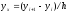
Доказательство. (4) получается в результате выполнения следующих преобразований
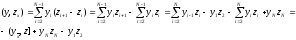
К равенству (5) приводят следующие преобразования
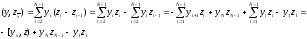
Сл-м (4) является
разностный аналог формулы Грина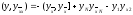 (6)
(6)
Очевидно, что в пространстве сеточных
функций, удовлетворяющих нулевым
граничным условиям, равенство (6) имеет
вид
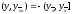 (7)
(7)
Заметим,
что в правой части (7) скалярное произведение
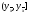 представляет собой линейный функционал,
удовлетворяющий аксиомам нормы:
положительная определенность;
линейность при умножении на скаляр;
неравенство треугольника.
представляет собой линейный функционал,
удовлетворяющий аксиомам нормы:
положительная определенность;
линейность при умножении на скаляр;
неравенство треугольника.
В силу этого наряду с нормами (1), (2)
полезным иногда представляется
использование нормы
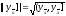 (8)
(8)
Утверждение
2. Для норм (1) и (8) справедлива
следующая оценка
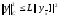 (9)
(9)
Доказательство.
Не нарушая общности, предположим, что
максимум абсолютного значения сеточной
функции достигается в k-том
узле сетки. Воспользуемся тождеством
(подставить вместо у с х с крышкой и
выйдет)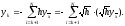
Для оценки пр. части этого равенства
используем неравенство Коши-Буняковского:
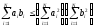 ,
полагая
,
полагая
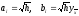 .
В результате приходим к
.
В результате приходим к
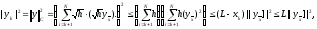 чтд.
чтд.
Задачи:
1)Определить
постоянные вложения векторных норм
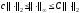 в пространстве
в пространстве
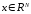 .
.
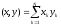
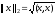 и
и
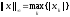
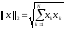
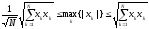
2)Доказать,
что матрица
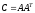 ,
,
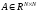 является симметричной.
является симметричной.
Квадратная матрица является симметричной, если она совпадает со своей транспонированной матрицей
3)Как связан спектр (множество собственных значений) диагональной матрицы и значения ее диагональных элементов (сумма собственных значений равна спектру, но т.к. она диагональная, то диагональные элементы и есть собственные значения).
4)Доказать, что число обусловленности матрицы не меньше единицы
Матричная норма должна удовлетворять следующим четырем аксиомам:
А4. || AB || ≤ || A || * || B || для любых матриц A и B.
Из последней аксиомы видно, что норма определена только для квадратных матриц (хотя, в приведенных выше формулах для вычисления различных норм, в принципе, нет такого ограничения). Кроме того, из последней аксиомы следует, что любая норма единичной матрицы I не меньше единицы, действительно || I || = || I*I || ≤ || I ||2 ⇒ || I || ≥ 1.
Тогда, опять с привлечением четвертой аксиомы, получаем, что число обусловленности матрицы всегда больше единицы (верно для числа обусловленности матрицы по отношению к произвольной матричной норме) 1 ≤ || I || = || AA-1 || ≤ || A || || A-1 || = cond(A).
5)Показать,
что при умножении
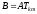 имеет место тождество
имеет место тождество
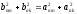 ,т.к.
,т.к.
6)Возможно ли с помощью степенного метода определить собственное значение действительной матрицы, если оно является комплексным? – нет. Будут одинаковые по модулю. Т.к. сопряжённый и комплексно сопряжённый.
1)Исследовать
устойчивость по начальным данным чисто
неявной схемы для уравнений теплопроводности:
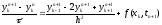 ,
,
Ищем
частное решение разностной задачи в
виде
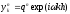 .
Подставим его в разностную схему при
.
Подставим его в разностную схему при
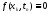 :
:
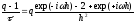 ,
откуда
,
откуда
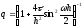 .
Очевидно, что при любых допустимых
значениях
.
Очевидно, что при любых допустимых
значениях
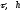 и
и
 постоянная
постоянная
 не превосходит по абсолютной величине
единицы => безусловно устойчива чисто
неявная схема, что означает устойчивость
при любых положительных
не превосходит по абсолютной величине
единицы => безусловно устойчива чисто
неявная схема, что означает устойчивость
при любых положительных
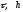 .
.
2)
Исследовать устойчивость трехслойной
схемы
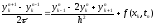
 =>
=>
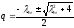 ,
где
,
где
 .
.
Отсюда
видно, что для любых положительных
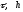 и для всех отличных от нуля
и для всех отличных от нуля
 по крайней мере один из корней
характеристического уравнения превосходит
по модулю единицу, что указывает на
отсутствие устойчивости дискретной
модели при любых шагах сетки.
по крайней мере один из корней
характеристического уравнения превосходит
по модулю единицу, что указывает на
отсутствие устойчивости дискретной
модели при любых шагах сетки.
