6.2. Разностная аппроксимация дифференциальных операторов. Сеточный шаблон. Явные и неявные схемы для нестационарных задач математической физики.

Разностная аппроксимация дифференциальных операторов - приближение ДУ системой алгебраических уравнений относительно значений искомых функций на некоторой сетке, которое уточняется при стремлении шага сетки к нулю.

Разностная схема аппроксимирует дифференциальную задачу, если погрешность аппроксимации данной разностной схемы на решении дифференциальной задачи стремиться к нулю при шагах сетки, стремящихся к нулю.

Множество точек сетки, на котором производится аппроксимация дифференциального оператора или дифференциальное уравнения, называют сеточным шаблоном или просто шаблон.

Правила, полезные при разностной аппроксимации дифференциальных уравнений:

- Разностные производные первого порядка на двухточечном шаблоне обеспечивают второй порядок аппроксимации в средней точке между задействованными узлами сетки.

- Разностные производные второго порядка на трехточечном равномерном шаблоне обеспечивают второй порядок аппроксимации в средней точке.

Разностные отношения называются соответственно правой, левой и центральной разностными производными функции u(x) в точке x_i , т.е. при фиксированном x_i  и h0 пределом этих отношений является u’(x_i).

Левая и правая разностные производные аппроксимируют u’(x) с первым порядком по h, а центральная разностная производная – со вторым порядком. Нетрудно показать, что вторая разностная производная аппроксимирует u’’(x_i) со вторым порядком по h:

Множество точек сетки, на котором производится аппроксимация дифференциального оператора или дифференциальное уравнения, называют сеточным шаблоном.

Главным недостатком явных схем численного решения нестационарных краевых задач математической физики следует считать чрезмерно жесткое условие устойчивости явных схем с постоянным по времени шагом, из-за которого они практически исключены из вычислительной практики. С другой стороны, при решении сложных задач реализация явных схем несравненно проще неявных, в которых решение приходится, как правило, находить более сложным путем - применяя итерации.

Рассмотрим задачу для нестационарного уравнения теплопроводности

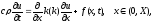
(1) с начальными и граничными условиями вида (2)

- некоторые заданные функции. Если 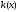не зависит от координат, то преобразуем (8) к виду 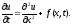(3)

Формально (1) преобразуется в (3) путем замены переменных: , .

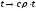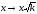Нужно решить (3) в области 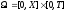, с начальными и граничными условиями (2).

Построим равномерную сетку :, . Множество узлов сетки представляет собой множество точек на плоскости с координатами ).

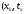Множество узлов сетки, соответствующих фиксированной 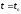- слой сетки. Множество узлов сетки, на которой ДУ аппроксимируется разностной схемой - шаблон схемы. определяется из начальных условий. Общая стратегия численного решения нестационарных уравнений в частных производных состоит в последовательном нахождении решения на временных слоях 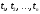. В этом смысле методика решения нестационарных задач математической физики во многом аналогична решению задач Коши для систем обыкновенных дифференциальных уравнений.

Построение схемы приближенного решения поставленной задачи сводится к тому, чтобы выразить приближенную зависимость значений искомой сеточной функции между слоями сетки. Пошаговое решение задачи состоит в том, чтобы, пользуясь построенной межслойной зависимостью вычислить значения искомой сеточной функции на верхнем временном слое по известным значениям сеточной функции на нижнем слое.

Если приближенный метод строится на основе только двух соседних слоёв сетки, то такие методы двухслойными (аналог одношаговых). Если шаблон схемы включает узлы сетки на n различных слоях, то схема называется n-слойной.

Один из способов выражения межслойных зависимостей значений искомой сеточной функции основан на использовании метода конечных разностей, суть которого состоит в замене непрерывных производных в дифференциальном уравнении на соответствующие разностные аналоги.

Рассмотрим уравнение (3) в произвольной внутренней точке сетки 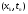. Используя разложение решения в степенной ряд в окрестности , выражаем точно частную производную второго порядка по пространственной переменной:

.

Аналогично, для первой производной по времени существует возможность использования разностные производные "вперед" или "назад":

I. ;

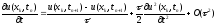II.

Заменяем соответствующие частные производные в (3) их разностными представлениями. В зависимости от того, какой из вариантов мы используем, приходим к двум вариантам разностной схемы. В первом случае мы приходим к разностной схеме:

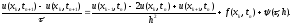(4)

Последний член полученного разностного уравнения характеризует погрешность аппроксимации данной разностной схемы: .

Предполагая, что шаги сетки достаточно малы и пренебрегая слагаемыми в погрешности аппроксимации, приходим к схеме: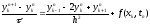(5)

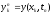- значения приближенного решения задачи в узле сетки .

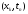(4) выражает зависимость между единственным зн-м 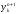искомого приближенного решения на верхнем слое и тремя зн-ми сеточной функции приближенного решения на нижнем временном слое. Такая особенность разностного уравнения позволяет явно выразить искомое решения из уравнения (5): (6)

Таким образом, нахождение искомого приближенного решения по схеме (5) сводится к вычислениям во всех внутренних узлах сетки по явным формулам (6). Решение в граничных точках вычисляются непосредственно из краевых условий.

Разностные схемы, допускающие непосредственное вычисление искомого приближенного решения по явным формулам вида (6), принято называть явными.

Используя второй способ аппроксимации производной с помощью разностной производной "назад", по аналогии с рассмотренным выше случаем мы приходим к следующей схеме 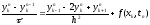, . (7)

В данном случае погрешность аппроксимации разностной схемы (7) на решении дифференциальной задачи (3), (2) также имеет порядок

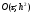
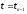В отличие от схемы (5), система разностных уравнений (7) не позволяет явно выразить искомое решение на верхнем слое через известные значения сеточной функции на нижнем слое . В этом случае нахождение приближенного решения задачи сводится к решению системы разностных уравнений, решающихся методом прогонки. Разностные схемы, для которых решения не может быть вычислено по явным формулам, а выражается СЛАУ принято называть неявными.