4.7. Коэффициент автокорреляции и проверка его значимости

Степень автокоррелируемости процессов измеряется коэффициентом автокорреляции, который устанавливает корреляционную связь между текущими и прошлыми наблюдениями временного ряда и рассчитывается по формуле

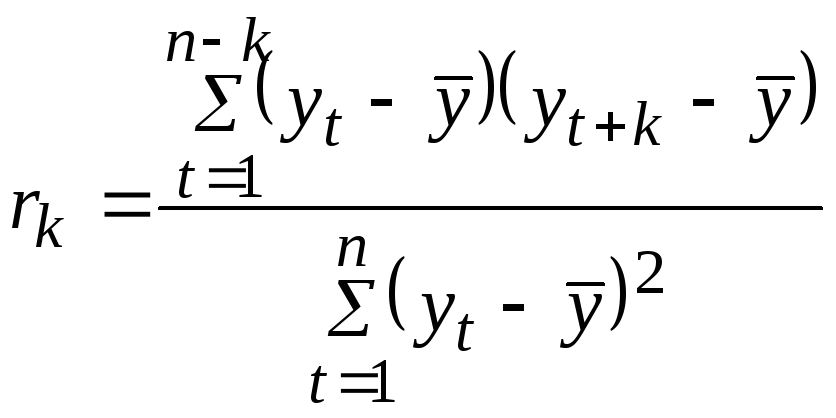, (4.14)

где – количество лагов (запаздываний). В соответствии с этой формулой коэффициент автокорреляции первого порядка рассчитывается при , второго порядка – при и т.д. При построении модели определяются коэффициенты автокорреляции всех порядков, и затем проводится статистическая проверка их значимости, чтобы установить с какими лагами следует включать в модель переменные.

Значимость коэффициентов автокорреляции принято проверять с помощью двух критериев: критерия стандартной ошибки и Q-критерия Бокса –Пирса.

Первый критерий используется для проверки значимости отдельного коэффициента автокорреляции. С его помощью удается выявить среди запаздывающих переменных те, которые необходимо включить в модель. Второй критерий позволяет сделать вывод о значимости всего множества переменных, включаемых в модель.

Суть проверки по первому критерию сводится к построению доверительного интервала для каждого -го коэффициента автокорреляции

.

Возможность построения такого интервала основана на том, что коэффициенты автокорреляции случайных данных обладают выборочным распределением, приближающемуся к нормальному с нулевым математическим ожиданием и средним квадратическим отклонением, равным . Если рассчитанное значение автокорреляции попадает в этот интервал, то можно сделать вывод, что данные не показывают наличие автокорреляции -го порядка.

Статистика для проверки по критерию рассчитывается по формуле

, (4.15)

где n – объем выборочной совокупности;

m – максимальный рассматриваемый лаг.

Статистика (4.15) имеет распределение с –степенями свободы и поэтому в случае, когда расчетное значение превосходит критическое значениес соответствующими степенями свободы, то, в целом, вся группа коэффициентов для лагов, не превосходящих , считается значимой.

4.8. Определение порядка моделей arma

Определение порядка авторегрессионной составляющей модели ARMA основано на проверке значимости коэффициентов автокорреляции. Кроме коэффициентов автокорреляции, при определении порядка авторегрессионной модели используются частные коэффициенты автокорреляции. Они лежат в основе построения частной функции автокорреляции и измеряют связь между текущими значениями переменной и последующим значениями этой же переменной , когда влияние всех промежуточных временных лагов устранено. В соответствии с этим определением частный коэффициент автокорреляции первого порядка будет равен коэффициенту автокорреляции первого порядка, так как в этом случае отсутствуют промежуточные лаги. Но частный коэффициент второго порядка будет отличаться от коэффициента автокорреляции второго порядка.

Частные коэффициенты автокорреляции используются для определения степени автокорреляции внутри временного ряда. Если процесс AR(m), то это значит, что последний статистически значимый частный коэффициент автокорреляции рассчитан с лагом . Следовательно, если при исследовании динамического процесса удается выяснить, что значения коэффициентов автокорреляции затухают по экспоненте, а частные коэффициенты автокорреляции значимо отличаются от 0 для временных лагов от 1 до , а для лагов, превышающих , резко падают до 0, то необходимо сделать вывод о построении авторегрессионной модели порядка .

Формальный вывод о затухающей динамике коэффициентов автокорреляции в случае авторегрессионной модели можно получить следующим образом. Рассмотрим модель процесса AR(1)

, . (4.16)

Последовательно подставляя в (5.16) соответствующие выражения для ,, …

. . . . . . . . . . . . . . . . . . . . . . .

, (4.17)

получим представление авторегрессионного процесса через случайные составляющие . С помощью этого представление определить основные статистические характеристики этого процесса: математическое ожидание, дисперсию, ковариацию.

При (процесс стационарный) и с учетом условий, которым удовлетворяет случайная величина математическое ожидание равно

. (4.18)

Введем обозначение и вычислим дисперсию

. (4.19)

Прежде чем вычислить коэффициент ковариации -го порядка, выполним операцию умножения, используя свойство независимости и опуская при перемножении те члены, математическое ожидание которых должно быть равно нулю

. (4.20)

Используя это выражение, получаем значение коэффициент ковариации -го порядка

. (4.21)

Из коэффициента ковариации легко получается соответствующий коэффициент автокорреляции

. (4.22)

Выражение (4.22) объясняет характер экспоненциального затухания значений автокорреляционных коэффициентов авторегрессионного процесса.

Формулы для вычисления значений частных коэффициентов автокорреляции очень громоздки, и поэтому пользоваться ими не очень удобно. В практике построения авторегрессионных моделей обычно принято пользоваться фактом, в соответствии с которым выборочное значение частного коэффициента автокорреляции можно вычислять как МНК-оценку последнего коэффициента авторегрессионного уравнения -го порядка

, (4.23)

т.е. . Статистическая значимость свидетельствует об отличии от нуля частного коэффициента автокорреляции.

Таким образом, авторегрессионный процесс первого порядка имеет следующие характеристики:

; ;

; . (4.24)

Его частная автокорреляционная функция порядка выше первого () должна быть равна нулю, в противном случае это авторегрессионный процесс не первого порядка.

По поведению коэффициента корреляции и частного коэффициента автокорреляции можно также определить, содержит ли временной ряд элемент скользящей средней. Если временной ряд скорее является MA, чем AR процессом, то с помощью коэффициента автокорреляции не удается установить порядок авторегрессионого процесса. Это следует из того, что модель скользящего среднего первого порядка МА(1)

, (4.25)

может быть представлена в виде авторегрессионого процесса AR(). С этой целью уединим в левой части уравнения и используем прием, который применялся при исследовании AR(1) модели,

. . . . . . . . . . . . . . . . . . . . . .

(4.26)

Полученное выражение при выполнении условия позволяет записать модель скользящего среднего в виде авторегрессионного уравнения бесконечного порядка

. (4.27)

Вычислим основные характеристики процесса МА(1):

; (4.28)

; (4.29)

. (4.30)

Получаем, что коэффициент автокорреляции первого порядка равен

. (4.31)

Причем для остальных все . Частные коэффициенты автокорреляции в соответствии со значениями коэффициентов авторегрессии (4.31) затухают по экспоненте.

Если проделать аналогичные вычисления для процесса МА(q), то получим, что его автокорреляционные коэффициенты для , т.е. их поведение аналогично поведению частных коэффициентов автокорреляции процесса AR(q). В то же время значения частных коэффициентов автокорреляции МА(q) процесса затухают по экспоненте точно так же как значения коэффициентов автокорреляции процесса AR(q).

Теперь перейдем к комбинированию процессов AR и МА. Модель простейшего смешанного процесса ARMA(1,1) может быть записана следующим образом:

, . (4.32)

Если выполняется и , то, как и в случае процессов AR(1) и MA(1), процесс ARMA(1,1) является стационарным и обратимым.

Вычислим основные характеристики этого процесса. Для этого выполним рекуррентные преобразования уравнения (4.32), предварительно перенеся в правую часть

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

. (4.33)

Используя полученное выражение, вычислим математическое ожидание процесса ARMA(1,1)

. (4.34)

Для вычисления дисперсии получим развернутое представление квадрата отклонения от математического ожидания через случайную составляющую

. (4.35)

Отметим, что в данном выражении не учтены те слагаемые, которые в силу свойства случайной составляющей должны обратиться в ноль при взятии математического ожидания.

Математическое ожидание выражения (4.35) дает нам дисперсию процесса ARMA (1,1)

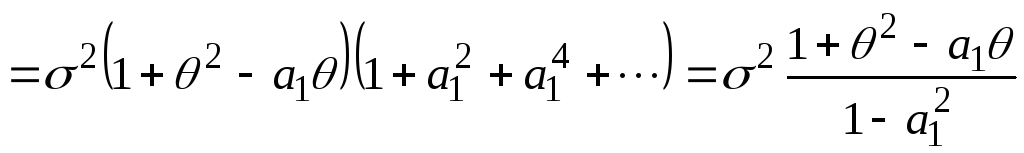. (4.36)

Наконец, для вычисления ковариации вычислим произведение, опустив в нем по аналогии с процедурой вычисления дисперсии те члены, которые при взятии математического ожидания должны обратиться в ноль

. (4.37)

После взятия математического ожидания получаем ковариацию первого порядка процесса ARMA (1,1)

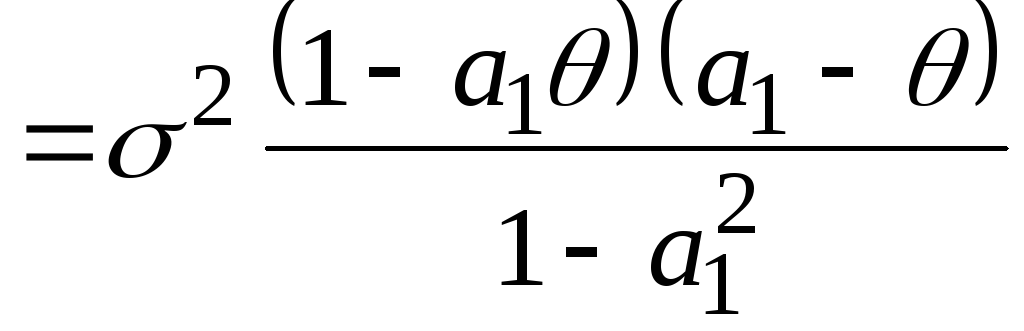. (4.38)

Ковариации более высоких порядков () могут рассчитываться в соответствии с рекуррентным соотношением

. (4.39)

Разделив ковариацию на дисперсию, получим коэффициент автокорреляции для процесса ARMA (1, 1)

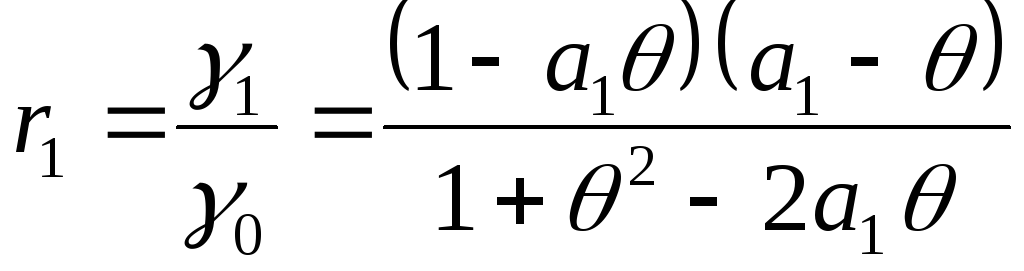, . (4.40)

Это представление свидетельствует о том, что коэффициенты автокорреляции ARMA (1, 1) ведут себя так же, как коэффициенты автокорреляции процесса AR(1). Этот вывод можно обобщить на случай процесса ARMA (p, q), для которого первые p значений автокорреляционных коэффициентов определяются взаимодействием AR и АМ компонент, а дальнейшее их поведение такое же, как в процессе AR (p).

Аналогичный вывод можно сделать для частных коэффициентов автокорреляции процесса ARMA (p, q). Они убывают точно так же, как частные коэффициенты автокорреляции процесса МА (q).