3.1.4. Парная регрессия как частный случай множественной

В практике прогнозных расчетов встречаются ситуации, когда находящиеся в распоряжении прогнозиста данные позволяют строить только однофакторные (парные) регрессионные модели. Так, если вспомнить, что применение построенной модели в прогнозных расчетах предполагает наличие значений независимых переменных на упреждающем отрезке, то становится понятным, почему иногда отказываются от построения сложных многофакторных моделей.

Процедура построения однофакторных моделей значительно проще, поэтому логикой изложения материала по регрессионному анализу, принятой в учебных пособиях, предусматривается рассмотрение сначала парной, а затем как ее обобщение – множественной регрессии. Причем, теория парной регрессии излагается в скалярном варианте, а множественной – в матричном. Здесь же, преследуя цель единообразия представления материала, парная регрессия рассматривается как частный случай множественной.

Используя обозначения

; ; ; ,

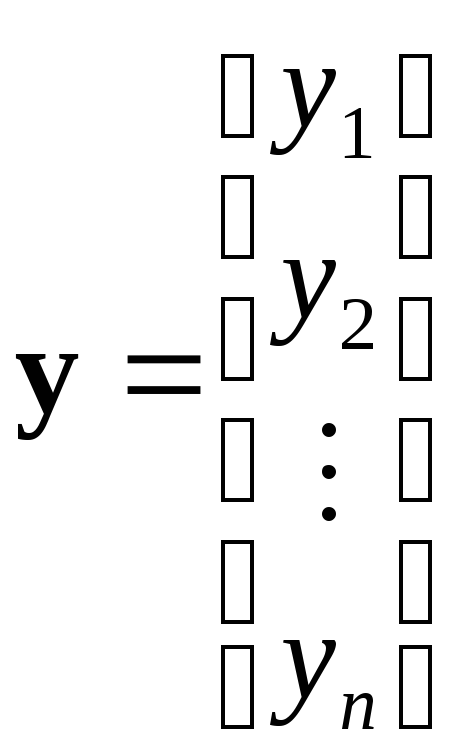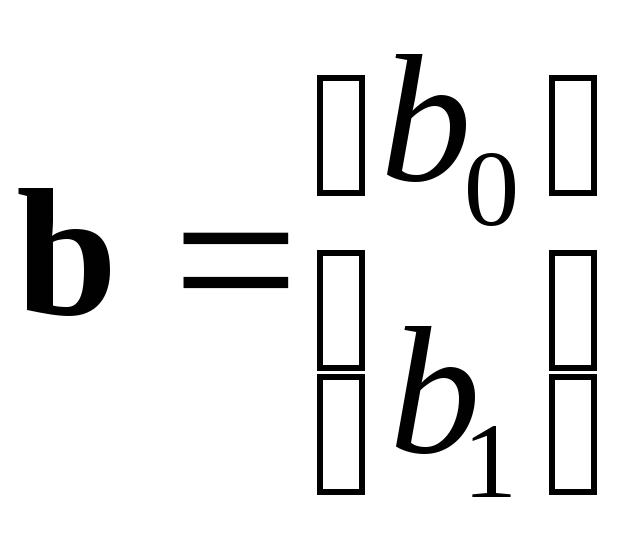систему нормальных уравнений для рассматриваемого случая в развернутом виде можно записать следующим образом:

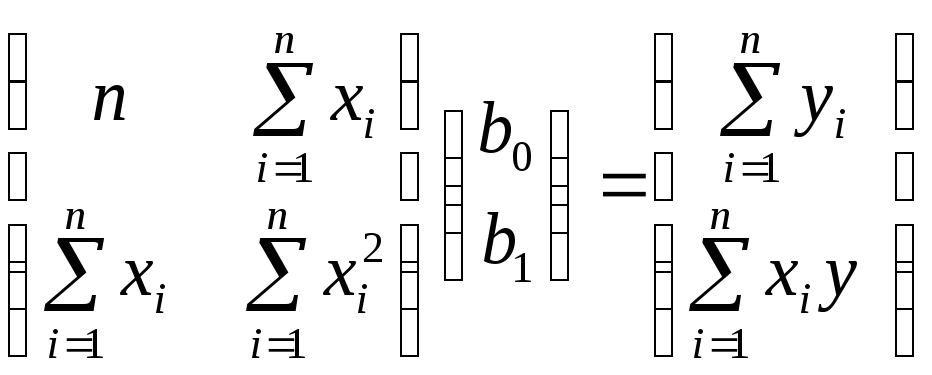. (3.33)

В общем виде решение этой системы вне зависимости от ее размера задается формулой (3.12). Однако больший интерес представляет решение, записанное в явном виде. Для системы (3.33), имеющей размеры , этот замысел легко реализуется. Сначала вычислим определитель

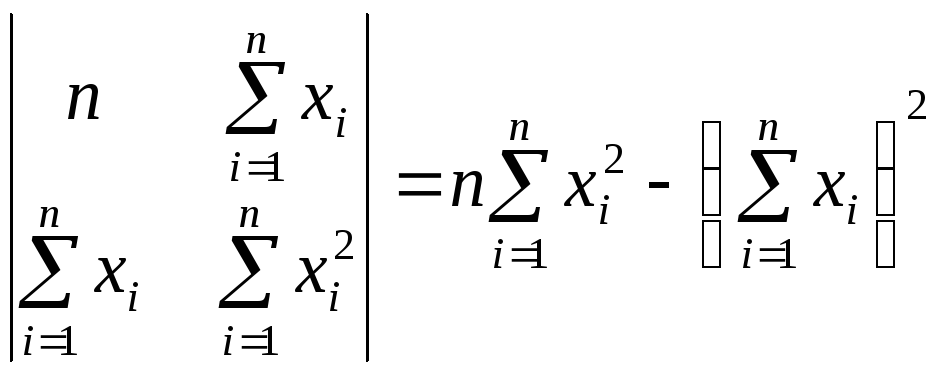(3.34)

а затем, используя полученное выражение, найдем обратную матрицу

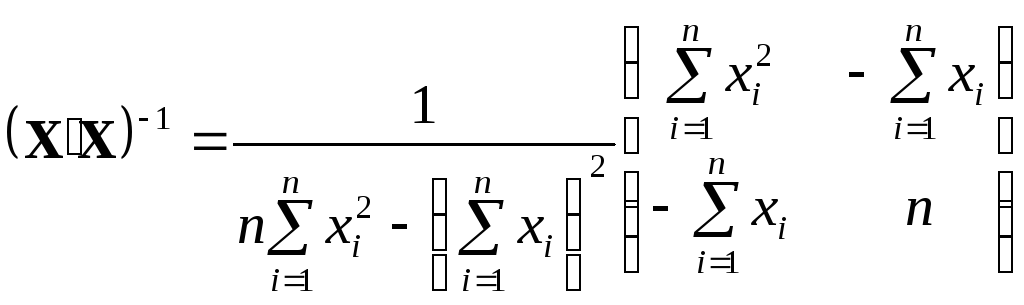. (3.35)

Тогда оценки коэффициентов парной регрессии могут быть записаны в виде

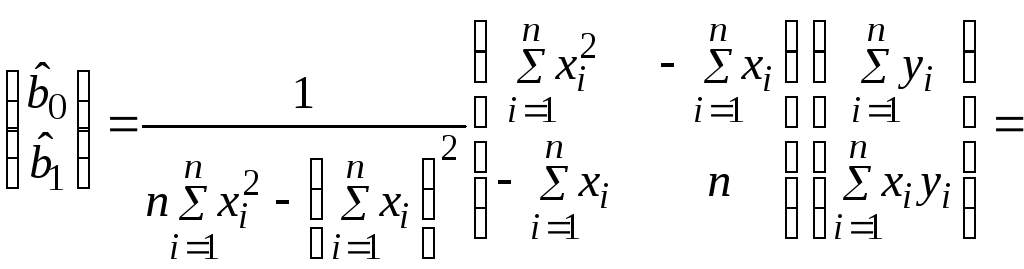
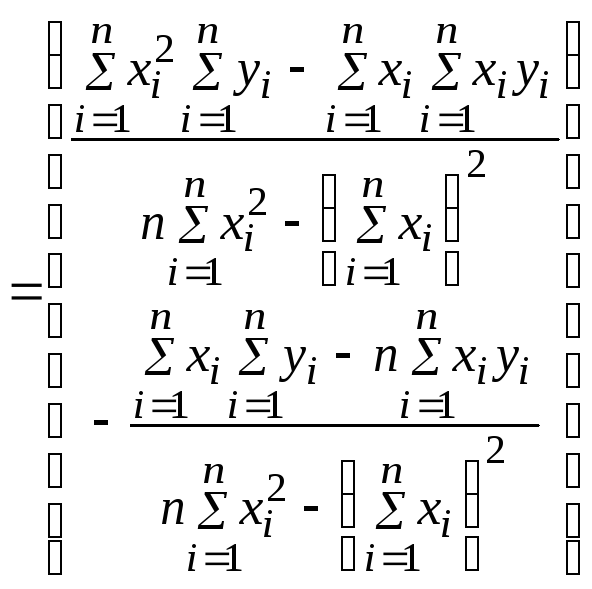. (3.36)

Если числитель и знаменатель каждой компоненты полученного вектора разделить на , то оценки коэффициентов могут быть записаны в привычном виде, через средние величины

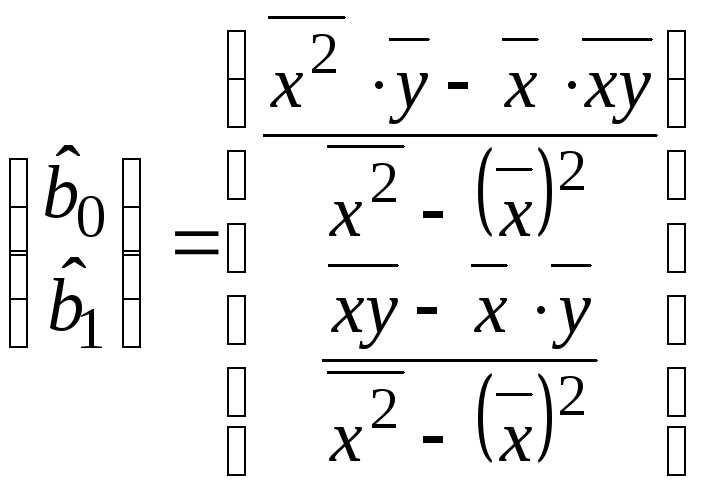. (3.37)

Для вычисления стандартных ошибок сначала получим оценку дисперсии случайной составляющей в виде остаточной дисперсии

, (3.38)

а затем, используя корни квадратные из диагональных элементов обратной матрицы, умноженной на остаточную дисперсию , запишем в явном виде выражения для вычисления стандартных ошибок оценок параметров регрессии

, (3.39)

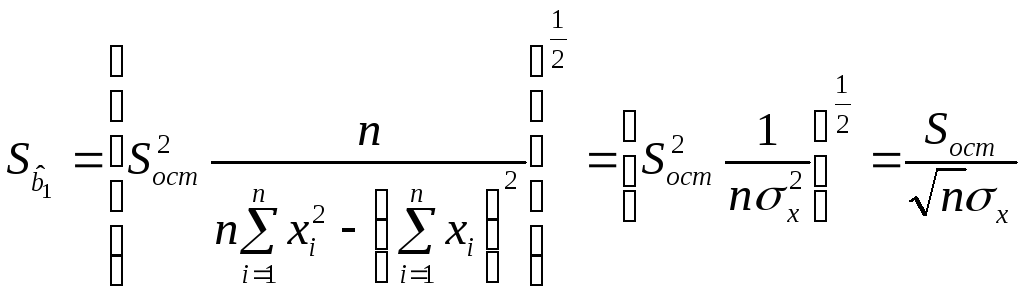. (3.40)

Таким образом, использование общей схемы МНК в матричной форме позволяет легко, следуя логике общей схемы, получить стандартные ошибки парной регрессии, записанных в виде (3.39), (3.40).

Стандартные ошибки используются, в частности, для расчета t-статистик Стьюдента

; , (3.41)

с помощью которых устанавливается, как и в случае множественной регрессии, статистическая значимость каждого коэффициента регрессии в отдельности. Кроме того, стандартные ошибки необходимы при расчете предельных ошибок

; , (3.42)

где – табличное (критическое) значение t-статистики Стьюдента при данных степенях свободы и выбранном доверительном уровне (см. Приложение).

Предельные ошибки, в свою очередь, применяются для определения доверительных интервалов:

; . (3.43)

Если границы доверительного интервала содержат 0, т.е. нижняя граница отрицательна, а верхняя – положительна, то оцениваемый параметр считается незначимым.

Для оценки качества регрессионного уравнения используются те самые показатели, что в случае множественной регрессии, но некоторые формулы расчета корректируются с учетом присутствия в модели только одного фактора. Например, коэффициент корреляции в случае парной регрессии рассчитывается по формуле

, (3.44)

где ; .

Значение коэффициента корреляции заключены между –1 и 1. При между показателем и фактором существует функциональная зависимость, при между показателем и фактором нет линейной связи, при имеет место корреляционная связь.