17

Федеральное агентство по образованию

Воронежский государственный университет

Математический анализ Числовые множества. Метод математической индукции.

Учебно-методическое пособие

по специальности 071900 «Информационные системы и технологии»

для студентов 1 курса очной формы обучения

Воронеж - 2006

Рекомендовано научно-методическим советом математического факультета ВГУ

Аннотация издания:

Пособие является второй из четырех частей учебно-методического пособия, созданного на основе опыта преподавания курса математического анализа на факультете компьютерных наук ВГУ. В него включен материал, относящийся к темам «Числовые множества» и «Метод математической индукции». Каждый параграф содержит справочный материал, набор типовых примеров с решениями и задачи для самостоятельной работы. В пособии приведены задания, предложенные студентам во время второй рубежной аттестации в 2004-2005 учебном году.

Авторы: к.ф-м.н, доцент Сергей Анатольевич Скляднев;

ассистент Светлана Вячеславовна Писарева

Научный редактор: д.ф-м.н, профессор Владимир Алексеевич Костин

Редактор: О.А. Тихомирова

 С.А. Скляднев, С.В. Писарева

 Воронежский государственный университет

§ 1. Множества

СПРАВОЧНЫЕ СВЕДЕНИЯ

1.1 Множества

Множества, как правило, обозначаются прописными буквами некоторого алфавита A, B, C, N, R,... Элементы же обычно обозначают строчными буквами a, p, e, x, t .... Знак " " обозначает принадлежность; запись "x M" читается "элемент х принадлежит множеству М". Если x не принадлежит множеству М, будем писать "x M", что читается "элемент x не принадлежит множеству М".

Буквами N, Z, Q, R обозначают, как правило, множества натуральных, целых, рациональных и действительных чисел соответственно.

Перечислим некоторые, наиболее употребляемые, способы задания множеств:

1. Множество может быть задано путем перечисления всех его элементов; например, множество всех цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; множество лиц, присутствующих сейчас в комнате {Коля, Володя, Ира, Лена, Оля}; множество всех трехзначных чисел в двоичной системе исчисления {100, 101, 110, 111} и т.п.

2. Множество М может быть задано путем формулирования некоторого характеристического свойства P(x), которым обладают элементы множества М (и только они одни): M = {x| P(x)} или M = { x: P(x)}.

Например, множество Е корней уравнения f(x)=0, где f(x) = x + 2x - 3x + 4 можно описать следующим образом: E = {x| f(x)=0}; множество А точек отрезка [0,1] можно описать так: А = {x: 0 x 1}.

3. Множество В может быть задано путем определения его элементов по уже известному множеству Т.

Например, считая заданным множество целых чисел Z = {.. -3, -2, -1, 0, 1, 2, 3, ...}, определим множество степеней числа 2: {..... 2 , 2 , 2 , 0, 2, 2 , 2 , .....}.

4. Различные операции над множествами, позволяющие из уже известных множеств получать новые (будут введены в дальнейшем).

Пустым называется множество, не содержащее никаких элементов. Оно обозначается символом Ø и содержится в любом множестве.

Множества А и В называются равными, если они состоят из одних и тех же элементов.

Если каждый элемент множества А является элементом множества В, то говорят, что множество А содержится в множестве В (пишут А В) или, что то же, множество В содержит множество А (пишут В А). В этих случаях говорят, что множество А является подмножеством множества В.

Очевидно, что для любого множества А: А А. Принято также считать, по определению, что пустое множество является подмножеством каждого множества: Ø А. Для любого множества А само А и пустое множество называются его несобственными подмножествами. Если же А Ø, А В и существует элемент хєВ такой, что х не принадлежит А, то А называется собственным подмножеством множества В.

Знаки " , " называются «кванторы»; запись " x M" читается "существует элемент х из множества М"; запись " x M" читается "для любого элемента х из множества М".

1.2 Операции над множествами

Пусть дано множество B={s}, называемое множеством индексов, и каждому индексу s сопоставлено множество A_s.

Объединением множеств А (α ) называется множество

А = { x| , х А }.

Очевидно, что для любого А: АUØ = А.

Пересечением множеств А (α ) называется множество

А = { x| , х А }.

Если множества С и D не имеют общих элементов, то С∩D=Ø. В этом случае, множества С и D называют непересекающимися.

Полезно отметить, что Ø∩Ø=Ø .

Разностью множеств А и В (А\В) называют множество, состоящее из тех элементов множества А, которые не принадлежат В. Ясно, что А\А=Ø.

На рисунке 1 серым цветом изображены последовательно множества A∩B, A B, А\В.

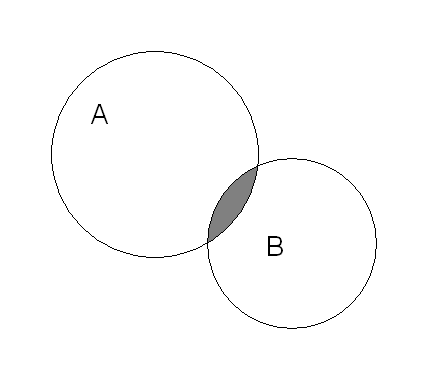
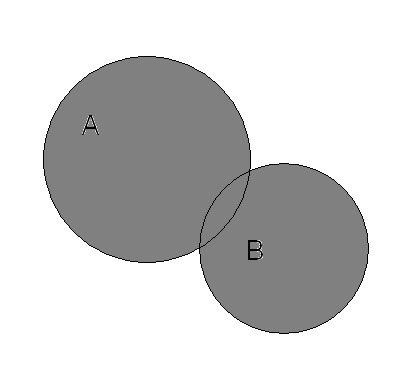
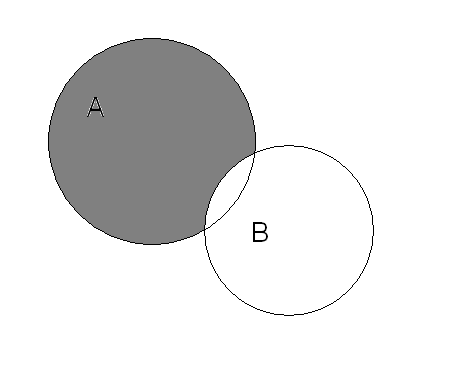
Рис.1 – Операции над множествами

Если В А, то А\В называется дополнением множества В до множества А.

В случае, когда рассматриваются различные подмножества множества А (и только они одни), дополнение множества В до множества А называются просто дополнением.

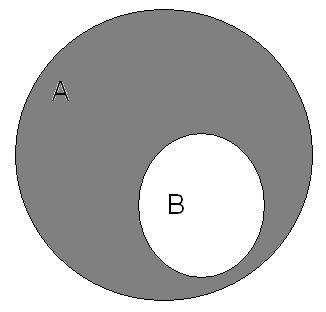
Рис.2 – Дополнение множества

1.3 Эквивалентные множества

Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если каждому элементу множества A сопоставлен один и только один элемент множества B, так что различным элементам множества A сопоставлены различные элементы множества B и каждый элемент множества B оказывается сопоставленным некоторому элементу множества A.

Множества, между которыми установлено взаимно однозначное соответствие, называют эквивалентными.

Если множества A и B эквивалентны, то пишут A~B.

Если AB_{1 ,} B₁B, и B не эквивалентно А, то говорят, что множество A имеет меньшую мощность, чем множество B .

Множество A называется конечным, если существует такое число n N, что

A~{1, 2, 3, …, n}.

В этом случае говорят, что множество A содержит n элементов или что множество A имеет мощность n.

Мощность пустого множества принимается равной нулю.

Множество, не являющееся конечным, называется бесконечным.

Множество A называется счетным, если A~N.

Множество называется несчетным, если оно имеет мощность, большую, чем мощность множества N.

Теоремы Кантора.

1. Множество всех рациональных чисел счетно.

2. Множество всех действительных чисел несчетно.

Множество A называется множеством мощности континуума, если A~R.

ПРИМЕРЫ С РЕШЕНИЯМИ

Пример 1. Даны множества A, B, C.

С помощью операций объединения и пересечения записать множество, состоящее из элементов, принадлежащих:1) всем трем множествам; 2) хотя бы одному множеству; 3) по крайней мере двум этим множествам.

Решение. 1) (A ∩ B) ∩C; 2) (A  B)  C; 3) (A ∩ B)  (C ∩ B)  (A ∩ C).

Пример 2. Найти АВ, А\В, В\А, АВ, если А={-4; -3; -2; -1; 0; 1}, В={-1; 0; 1; 2; 3}.

Решение. АВ={-4; -3; -2; -1; 0; 1; 2; 3}; АВ={-1; 0; 1}; А\В={-4; -3; -2}; В\А ={2; 3}.

ЗАДАЧИ

Задача 1. Доказать, что включения А В и В А выполняются одновременно тогда и только тогда, когда А=В.

Задача 2. Докажите, что равенства : 1) А  В = В ; 2) А ∩ В = А; верны тогда и только тогда, когда A  B.

Задача 3. Докажите, что (А\В)∩(В\А)=Ø.

Задача 4. Докажите, что любое непустое множество имеет не менее двух подмножеств.

Задача 5. Докажите, что если А В и В D, то A D.

Задача 6. Докажите, что если а А, то одноэлементное множество {а} А.

Задача 7. Докажите, что равенство A\ (В \ С) = (A \ B)  С верно тогда и только тогда, когда А  С.

Задача 8. Докажите равенство A\ (A \ B) = A  B.

Задача 9. Докажите, что АU(BUC)=(AUB)UC.

Задача 10. Докажите, что A∩(BUC)=(A∩B)U(A∩C).

Задача 11. Докажите, что A∩(BUA)=A.

Задача 12. Докажите, что AUA=A.

Задача 13. Докажите, что A∩A=A.

Задача 14. Докажите, что (A \ B)  (B \ A) = (A  B) \ (A  B).

Задача 15. Докажите, что (A \ B) \ C= A \ (B  C).

Задача 16. Докажите, что (A \ B)  C = (A  C) \ (B  C).

Задача 17. Докажите, что A  (B \ C)  (A  B) \ C.

Задача 18. Докажите, что (A  C) \ B  (A \ B)  C.

Задача 19. Докажите, что X\( A )= (X\A ).

Задача 20. Докажите, что X\( A )= (X\ A ).

Задача 21. Найти А  В, А \ В, В \ А, А  В, если А={-1;0;1;2;3;4;5}, В={2;3;4;5}.

Задача 22. Найти А  В, А \ В, В \ А, А  В, если А={-1;0;1;2;3}, В={-2;-1;0;1}.