3.3. Регрессионные модели с автокоррелированными остатками

3.3.1.Общая схема мнк в случае автокорреляции первого порядка

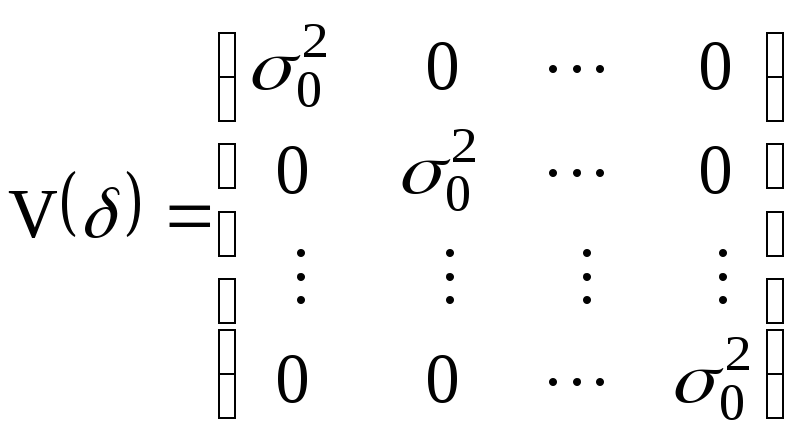
Чаще других при построении прогнозных моделей регрессии используются данные, представляющие собой временные ряды. В случае временных рядов нарушение условия 3b) состоит в том, что случайные остатки коррелируют между собой и, следовательно, матрица становится недиагональной. Поэтому рассмотренный выше метод взвешенных наименьших квадратов к данной ситуации не применим, т.е. возникает необходимость в применении другого варианта обобщенной схемы МНК, отличного от случая гетероскедастичности. Начнем с рассмотрения простейшего случая, когда зависимость между остатками , выражается автокорреляцией первого порядка, т.е.

, (3.92)

где , а – случайная величина, удовлетворяющая условиям классической регрессии

, . (3.93)

Кроме того, будем считать, что соотношение (3.92) справедливо для любого t ().

Учитывая свойства случайной составляющей , описываемые соотношениями (4.93), вычислим основные ее числовые характеристики и . Для этого представим случайную величину в виде бесконечного ряда

. (3.94)

Используя полученное представление и свойство (3.93), получаем

, (3.95)

. (3.96)

При вычислении дисперсии было учтено, что между собой независимы и поэтому математические ожидания произведений при равны 0.

Чтобы вычислить ковариационную матрицу, вычислим произведение при произвольном . Для этого предварительно первый сомножитель представим в виде двух слагаемых.

. (3.97)

Произведение первого слагаемого и второго сомножителя равно 0 в силу того, что , т.е.

. (3.98)

Таким образом, если снова учесть, что независимы, то ковариация между и будет равна

, (3.99)

где дисперсия определяется соотношением (3.96).

Мы получили представление о структуре ковариационной матрицы случайной составляющей модели с автокоррелированными остатками. Выражение (3.96) задает ее диагональные элементы, а (3.98) – внедиагональные элементы ковариационной матрицы.

Обобщая проведенные исследования, можно записать условия, в которых строится регрессионная модель с автокоррелированными остатками:

1. Спецификация .

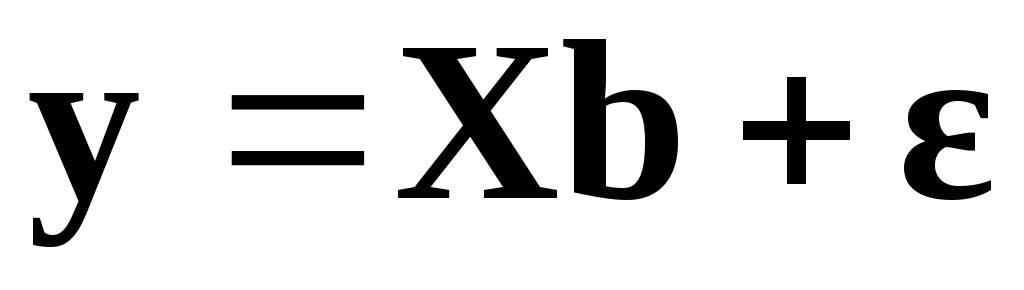2. – детерминированная матрица 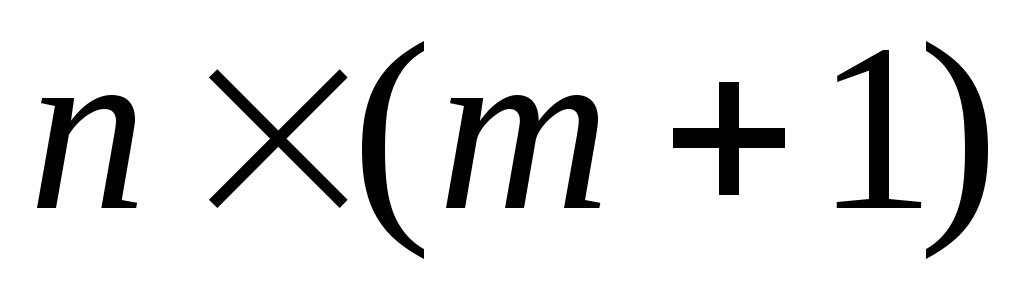с рангом .

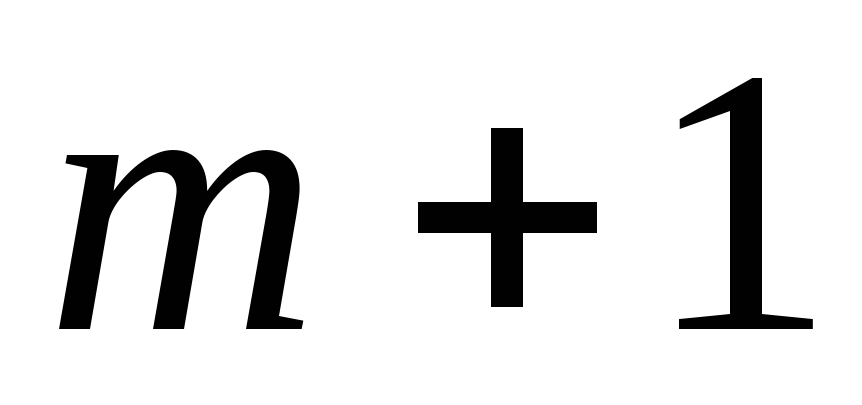3а. . 3b. .

Для удобства изложения материала введем обозначение

. (3.100)

Матрица симметрична и положительно определена (, -произвольный ненулевой вектор). Так как по определению коэффициент корреляции между остатками равен

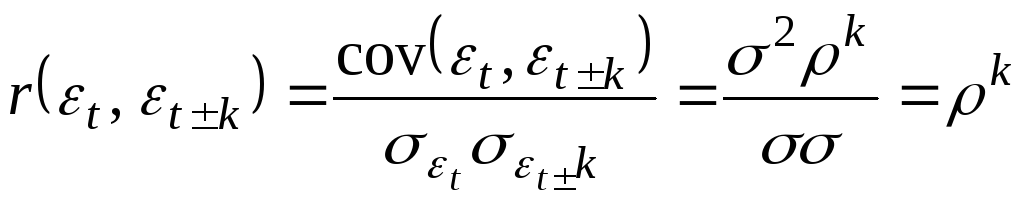, (3.101)

то можно сделать вывод о том, что в линейной модели с автокоррелированными остатками в такой математической форме реализована идея ослабления корреляционной связи между регрессионными остатками по мере их взаимного удаления во времени.

Так как в дальнейшем потребуется , то приведем ее общий вид

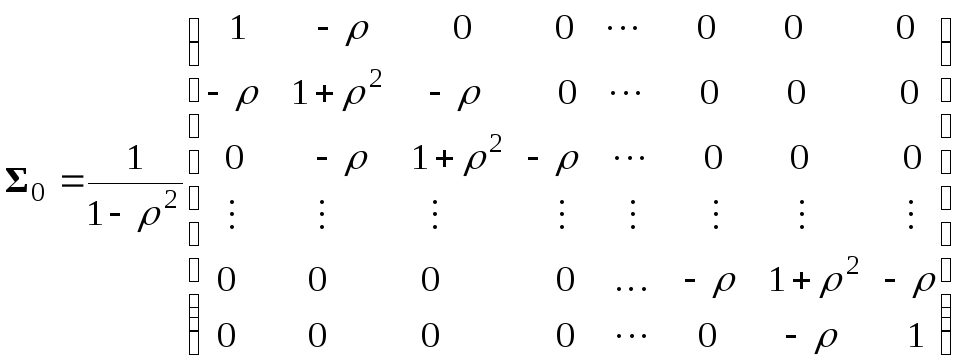. (3.102)

Зная обратную матрицу (3.102), можно записать, используя схему обобщенного МНК, формулу для вычисления оптимальных оценок в классе несмещенных в следующем виде:

. (3.103)

Так как по условию симметрична и положительно определена, то и также симметрична и положительно определена. Следовательно, ее можно представить как

, (3.104)

где – диагональная матрица, на главной диагонали которой стоят собственные значения матрицы , а – ортогональная матрица, столбцы которой представляют собой собственные вектора , т.е. .

Поскольку положительно определенная матрица, ее собственные числа положительные и, следовательно, можно определить дробную степень в виде

, (3.105)

где – диагональная матрица с элементами по главной диагонали.

Введение дробной степени позволяет представить матрицу в виде произведения двух матриц

. (3.106)

Такое представление позволяет записать формулу обобщенного МНК в виде:

, (3.107)

где , .

Для рассматриваемого случая матрица может быть записана следующим образом:

. (3.108)

Преобразование данных с помощью этой матрицы приводит к следующим результатам:

; (3.109)

. (3.110)

Таким образом, если известно, что между остатками наблюдается автокорреляция и известен параметр , то после преобразования данных в соответствии с (3.109), (3.110) для оценки параметров регрессии можно применить обычный МНК, который, по сути, является частным случаем обобщенной схемы МНК.

Следовательно, чтобы принять решение о методе построения регрессионного уравнения по данным временных рядов, необходимо сначала установить наличие автокорреляции в остатках, а затем получить оценку параметра .