13. Построение частотных характеристик

Для произвольных линейных систем применение частотных характеристик обязательно включает операцию перехода к преобразованию Лапласа. Запишем формулу передаточной функции:

Если от аргумента s =  + jперейти к аргументуs = j, положив = 0, то будем иметь дело с моделью в виде частотной передаточной функции:

Q₁ = a_o - a₂ ² + a₄ ⁴ - ... Q₂ = a₁ - a₃ ³ + a₅ ⁵ - ...

P₁ = b_o - b₂ ² + b₄ ⁴ - ... P₂ = b₁ - b₃ ³ + b₅ ⁵ - ...

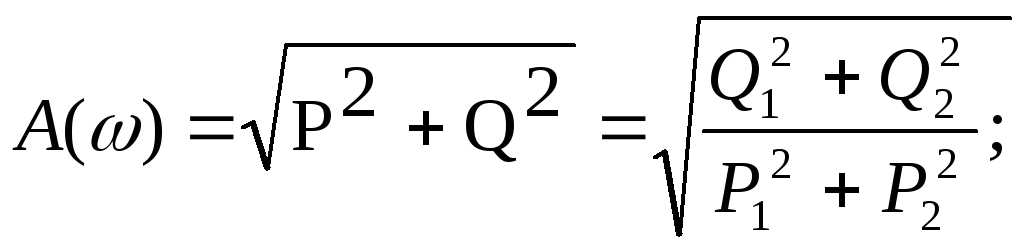
Меняя частоту от0доможно строить частотные характеристики, по виду которых анализируется качество работы схемы. Итак, в общем виде

амплитудно - фазовая характеристика имеет вид:

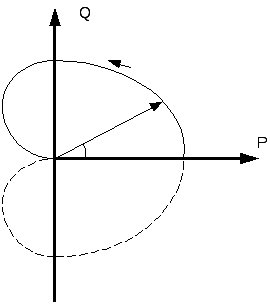
Отметим, что динамика стационарных линейных систем в плане анализа устойчивости и быстродействия полностью может быть исследована с помощью частотных характеристик. Однако, применение частотных характеристик для произвольных линейных систем не всегда рационально. Такой выбор должен быть обоснован.

2. Методы анализа качества систем управления

   1. Понятие устойчивости систем управления

Комплекс требований, определяющих поведение САУ, объединяется понятием качества процесса управления (качества системы управления). Главным требованием, предъявляемым к качеству работы систем управления, является требование устойчивости. Рассмотрим основные положения теории устойчивости.

Если под действием возмущения система управления отклонилась от состояния равновесия или заданного закона движения, а после прекращения действия возмущения снова вернулась к исходному состоянию, то такое движение является устойчивым, сходящимся к исходному. Если по окончанию воздействия, как бы мало оно не было, управляемая координата продолжает изменяться, или, если по окончании воздейсвия устанавливается новое состояние равновесия, отличное от первоначального, зависящее от произведенного воздейсвия, то объект является неустойчивым. Объект, способный после кратковременного внешнего воздействя с течением времени возвратиться к исходному состоянию или близкому к нему является ассимптотически устойчивым.

Рассмотрим определение устойчивости по Ляпунову [1]. Пусть имеем уравнение динамики:

.

Его можно переписать с использованием фазовых координат:

.

,

- фазовые координаты, характеризующие состояние системы. Их можно трактовать как координаты n– мерного пространства. Такое пространство называется пространством состояний, и его координаты представляют собой производные по времени. Координатывектора состояния – это абстрактные величины, лишенные физического смысла. Представленное уравнение в фазовых координатах описывает невозмущенное движение. Полагаем, что фазовые координаты в начальный момент времениt = t_o имеют значения:x₁ = ₁ (t₀), x₂ = ₂ (t₀), ... , x_n = _n (t₀). Решение дифференциального уравнения определяется введенными начальными условиями. Оно может быть записано в виде

x_i =_i [t,_i(t_o)] .

Пусть под действием возмущения начальные значения координат изменились и приняли значения:

 _i^*(t_o) =_i(t_o) +_i .

Характер процессов, происходящих в системе, будет описываться уравнениями вида:

x_i^* =_i^*[t,_i^*(t_o)] .

Последнее уравнение описывает возмущенное движение. Движение называется устойчивым по Ляпунову, если при небольших изменениях начальных значений возмущенное движение в момент времениt > t₀будет отличаться от невозмущенного движения незначительно. Другими словами, движение, определяемое решением, будет устойчивым по Ляпунову, если для любого > 0 можно подобрать () > 0, чтобы приt > t₀ и при

|  _i^*(t_o) -  _i (t_o) | <  ()

выполнялось условие:

|  _i^*(t) -  _i (t) |  .

Если условие не выполняется, то движение неустойчиво. Движение считается асимптотически устойчивым, если при t

lim| _i^*(t) - _i(t) | = 0.

Отметим, что линейная система в подавляющем большинстве случаев получается в результате линеаризации характеристик исходной нелинейной системы, то есть является ее приближенной моделью, вследствие этого возникает вопрос – правомерно ли переносить выводы об устойчивости линейной системы на исходную нелинейную систему, когда и в какой мере это справедливо. А.М. Ляпуновым был доказан ряд теорем, отвечающий на поставленный вопрос.

Теорема 1.Если вещественные части всех корней характеристического уравнения первого приближения являются отрицательными, то невозмущенное движение в исходной нелинейной системе асимптотически устойчиво независимо от отброшенных при линеаризации членов.

Теорема 2.Если среди корней характеристического уравнения первого приближения есть хотя бы один, имеющий положительную вещественную часть, то невозмущенное движение неустойчиво независимо от отброшенных при линеаризации членов.

В тех случаях, когда в характеристическом уравнении есть нулевые или чисто мнимые корни, а все остальные корни имеют отрицательные действительные части, судить об устойчивости движения по уравнению первого приближения нельзя. В таком случае для оценки устойчивости необходимо учитывать отброшенные при линеаризации нелинейные слагаемые.

Другими словами стационарная линейная система управления, поведение которой описывается обыкновенными дифференциальными уравнениями, устойчива тогда и только тогда, когда все корни ее характеристического уравнения (полюсы ее передаточной функции) имеют отрицательные вещественные части, то есть лежат в левой полуплоскости комплексной переменной s.

Характеристическое уравнение системы управления, исследуемой в комплексной области, представляется выражением:

b_nsⁿ + b_n-1s ^n-1+ ... + b_o = 0.

Если система управления исследуется в области фазовых координат, то характеристическое уравнение рассматривается в виде:

det[sE-A] = 0,

где A– матрица коэффициентов уравнений в фазовых координатах;E- единичная матрица;s - алгебраическая переменная.

В теории автоматического управления пользуются условиями, которые позволяют судить о расположении корней характеристического уравнения в левой полуплоскости без нахождения их значений. Что весьма существенно, так как корни уравнений выше четвертой степени не выражаются через коэффициенты посредством алгебраических соотношений и могут быть найдены лишь численно. Такие условия называются критериями устойчивости. Существует несколько критериев устойчивости. Все они математически эквивалентны, так как решают единственный вопрос – лежат ли все корни характеристического уравнения в левой полуплоскости или нет. Существующие критерии устойчивости делятся на две группы: алгебраические и частотные.