3. Расчет и анализ чувствительности

Основной задачей теории чуствительности является анализ дополнительного движения вызванного вариацией параметров. Такой анализ, в частности, включает количественные оценки, характеризующие влияние одних параметров на другие или на качество технической системы в целом. Обычно анализ дополнительного движения строится на основе нахождения функций чувствительности, получаемых в результате решения дифференциальных уравнений называемых уравнениями чувствительности. Вместе с тем применяются различные косвенные оценки, в том числе частотные или корневые. Будем рассматривать моделирование динамики системы управления в комплексной плоскости. Вектором параметров, по отношению к которому требуется оценить чувствительность системы управления, выберем вектор p.Компонентами вектора могут быть коэффициенты передаточных функций элементов управляющей части системы или объекта управления. В качестве исследуемой характеристики, изменяющейся при вариацииp,выберем управляемую переменнуюy на выходе объекта управления. Тогда чувствительностьyкpможет быть представлена вектором

(6.5)

для системы управления, описываемой системой уравнений вида

Y(p,s) =W(p,s)G(s).

(6.6)

В формуле (6.5) v – размерность вектораp, - начальное (номинальное) значение параметра,- установившееся значение выходного сигнала при. Частные производные, входящие в формулу (6.5), вычисляются в точке.

Рассмотрим вопрос количественной оценки чувствительности установившегося режима к вариации параметров вектора p. Для этого положимs = 0иG(s) = 1/s. В силу принятых допущений выражение (6.5) значительно упростится без потери существенной информации относительно установившегося режима:

(6.7)

Расчет чувствительности включает этапы:

• задание структуры и состава системы управления, вектора ;

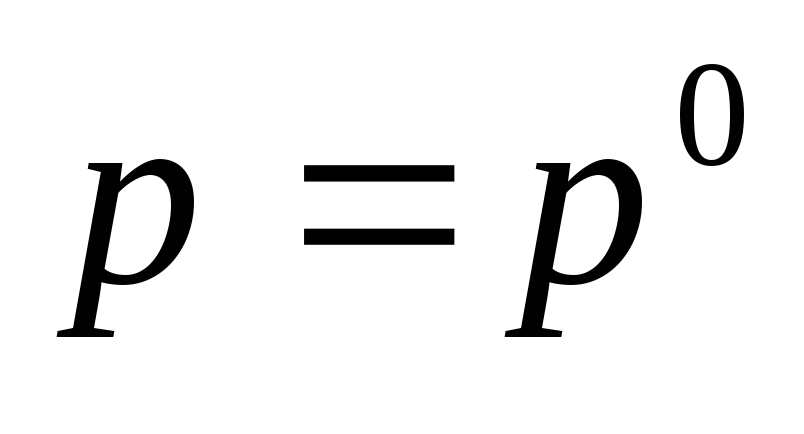• построение W(p,s);

• формирование ;

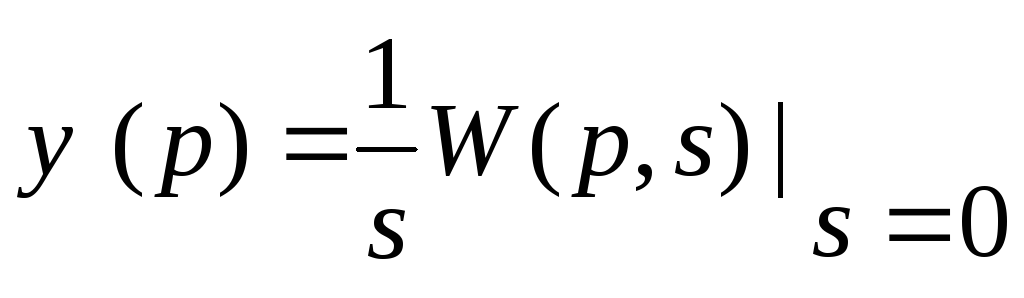• определение .

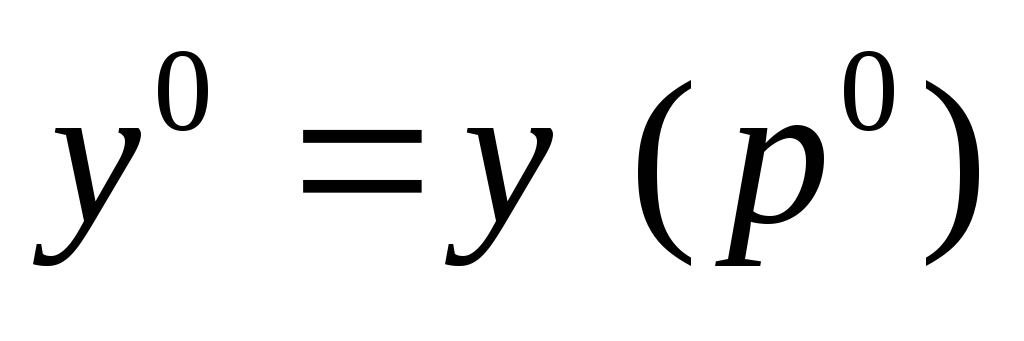• вычисление чувствительности по формуле (6.7).

Если анализ диктует необходимость рассмотрения функций чувствительности для установления влияния вектора pна динамику системы управления, тоsв формуле (6.7) не должно обнуляться и от полученных функцийследует перейти к временным функциямна основе известного разложения Хевисайда рациональной алгебраической функции.

4. Робастные системы управления

Проектирование робастных систем управления – одна из сложных проблем современной теории управления. Свойство систем управления обеспечивать устойчивость при вариации параметров объекта управления в определенных пределах называется робастной устойчивостью. Отметим, что устойчивость является одним из самых важных свойств систем управления, но не единственным. Такие важные характеристики управления как точность, время регулирования, перерегулирование должны обеспечиваться также на приемлемом уровне. Свойство системы управления выполнять заданные требования на качество при вариации параметров объекта управления можно определить как свойство робастности в более широком смысле, чем робастная устойчивость. Ограничения на качество управления могут назначаться как во временной, так и в комплексной области. Для исследования робастной устойчивости систем управления на практике используется подход, базирующийся на результатах теоремы Харитонова, дающий заключение о робастной устойчивости на основе алгебраического анализа корней четырех полиномов.

Рассмотрим вопрос проектирования робастно устойчивых систем управления с заданным качеством управления. Представим передаточную функцию в виде

,

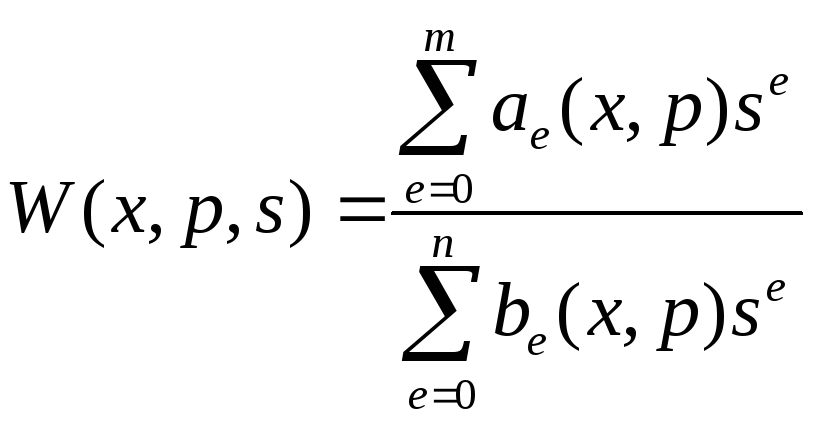где х– вектор настраиваемых параметров управляющей части,p - вектор квазистационарных параметров объекта управления. Пусть

Границы включают номинальные значения параметров, а также их возможные вариации под действием внешних и внутренних факторов. Для того чтобы найти зависимостьх = х (p), которая бы позволяла настраиватьхпо известным реализациямp, обеспечивая требуемое качество управления, воспользуемся моделированием процессов в комплексной плоскости, что позволит сформировать целевую функцию

на основе приближения проектируемой системы управления к эталоной. Введем в рассмотрение семейство полиномов:

где АиB– являются полиномами числителя и знаменателя передаточной функции с коэффициентами вида:,.

Если компоненты векторов х иpнаходятся внутри своих границ, то и коэффициенты,(i =1,…,m; j = 1,…n)тоже могут варьироваться только внутри своих собственных границ, зависящих отхиp, посколькуa иb являются однозначными функциями переменныххиp, то есть

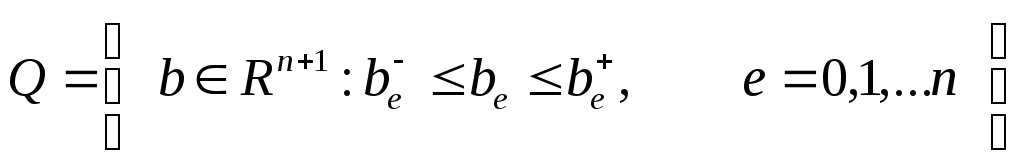
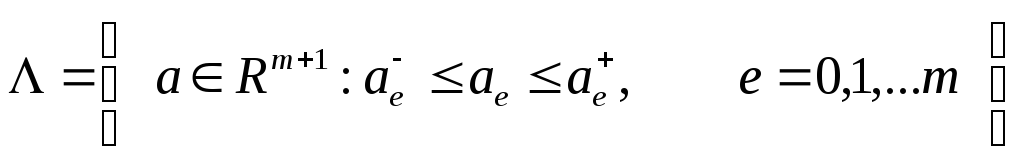
Будем считать [6], что система управления является робастно устойчивой и имеет заданное качество управления, если семейства ее полиномов иB(s,Q)удовлетворяют требованиям (3.8) – (3.9). Их сказанного следует, что семействоB(s,Q)робастно устойчиво тогда и только тогда, когда для любой реализации векторакорни полиномаB(s,b)располагаются в левой полуплоскостиs. Отметим, что значения компонент вектораb определяются путем подстановки в их выражения значенийи

Теорема.Для того чтобы многомерная система управления являлась робастно устойчивой и удовлетворяла заданным динамическим характеристикам (3.9) достаточно, чтобыF(x,p) = 0при

.

Доказательство.Следуя от противного, предположим, что качество управления оптимизированной по параметрам системы управления неудовлетворительно приF(x,p) = 0, где . Это означает, что расположение полюсов и нулей, соответствующее решению, не удовлетворяет требованию (3.9). Следовательно, существует, по крайней мере, один полюс или нуль отличный от идеального. В рамках правила формирования целевой функцииF(x,p)это означает, что она имеет хотя бы одно слагаемое отличное от нуля, что противоречит условию теоремы.

Рассмотрим процедуру определения запаса робастности. Считаем известными номинальные значения компонент вектора pи возможные границы его вариации, а также считаем известным аналитическое выражениеB(x,p,s). Задача состоит в том, чтобы вычислить запас робастности системы управления при. Другими словами, из более широкой области границP, внутри которых качество системы управления неизвестно, нужно выделить подобласть, то есть такие границы, при которых семейство полиномов

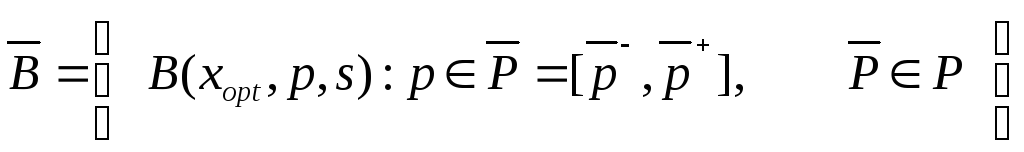
будет робастно утойчивым. Величину

, ,

(6.8)

будем считать мерой запаса робастности. Рассмотрим сказанное на простом примере. Пусть номинальные значения вектора варьируемых параметров равны . Наименее допустимое отклонение параметров от номинальных значений до границ интервалов составляет 1.0, то же самое значение дает формула (6.8). То есть, если параметры будут отклоняться на величину равную 1.0 или менее ее, то система управления сохранит свое качество.

Обратимся к интерпретации теоремы Харитонова. Доказано, что если корни четырех полиномов:

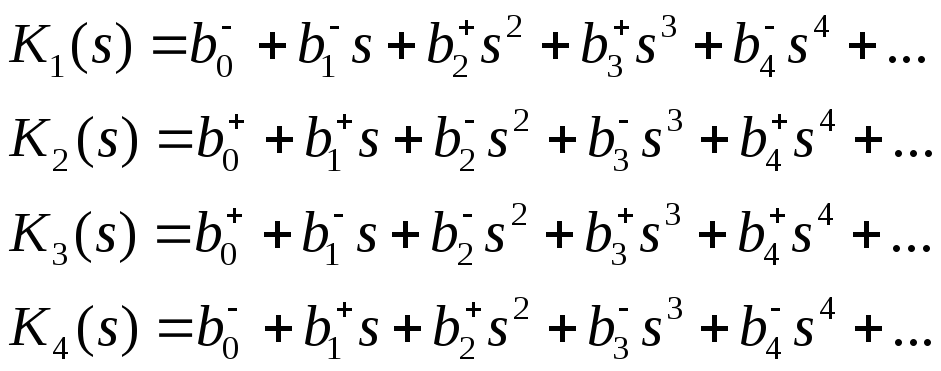
полученных из полинома характеристического уравнения, имеют отрицательные действительные части, то система управления будет сохранять устойчивость при вариации вектора p внутри границ назначенных интервалов.