5. Дискретные и цифровые системы управления

   1. Общие сведения

Линейной системой импульсного регулирования называется такая система автоматического регулирования, которая кроме звеньев, описываемых обыкновенными линейными дифференциальными уравнениями, содержит импульсное звено, преобразующее непрерывное входное воздействие в равноотстоящие друг от друга импульсы. Рассмотрим принцип работы дискретных систем управления, которые наряду с цифровыми относятся к импульсным системам. Будем считать [5], что квантование сигналов х(t)по времени осуществляется с постоянным интервалом (периодом)Т, и сигналы дискретной системыx(kT)представлены последовательностями идеальных импульсов различной амплитуды, определенных в равноотстоящие моменты времениt = kT. Целое число

k = 0,1,2,…называется дискретным временем, а сами амплитудно - модулированные импульсные последовательности - решетчатыми функциями. С целью упрощения обозначений дискретные сигналы рассматриваемого типа часто записываются просто как функции дискретного времениx(k), т.е.

.

Описание дискретного процесса может быть представлено как решение разностного уравнения. Наиболее распространены разностные уравнения

n– го порядка (модели вход – выход) и системы уравнений первого порядка

(модели вход – состояние - выход), а также их операторные формы. Дискретные модели либо отражают динамику реальных квантованных по времени процессов, либо являются одной из форм приближенного описания систем непрерывного действия. В последнем случае возникает необходимость рассмотрения вопросов квантования и методов преобразования динамических систем к дискретной форме, т.е. их дискретизации.

2. Модели дискретных процессов

Разностные уравнения, описывающие динамику систем дискретного времени получаются в результате анализа реальных процессов в различные моменты дискретного времени k.

Пример 5.1.Рассмотрим цифровой накопитель (счетчик), содержимое которого в дискретные моменты времениkописывается функцией

с начальным значением . В моментk на вход счетчика поступает сигнал, в результате чего в последующий момент дискретного времениk + 1происходит увеличение содержимого счетчика на величину этого сигнала:

(5.1)

Последнее выражение и является моделью счетчика, представленной в форме разностного уравнения первого порядка. Уравнение (5.1) можно записать в операторной форме. Введем в рассмотрение оператор сдвига (упреждения) z, действующий по схеме

и после элементарных преобразований получим

(5.2)

Оператор 1/(z - 1)является передаточной функцией дискретной системы (5.1).

Пример 5.2.Проанализируем прохождение однородных предметов (товаров) в торговой системе склад – магазин, функциональная схема которой представлена на рисунке

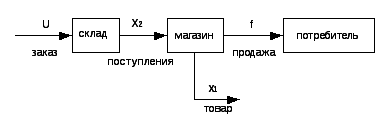
Рис. 5.1. Система склад – магазин

Здесь - число товаров в магазине,- товары, поступающие со склада,- заказанное количество товаров (заказ),- число реализованных (проданых) товаров,k– дискретное время в днях. Начальное состояние системы (в моментk =0) характеризуется значениямии.

Динамика товаров в магазине описывается разностным уравнением

(5.3)

в котором число проданных единиц товара f(t)выступает в роли возмущающего воздействия. Полагая, что заявка выполняется складом с задержкой в один день, запишем модель склада в виде

(5.4)

где заявка u(k)на требуемое количество товара играет роль управляющего воздействия. Если задача управления ставится как задача регулирования объема товаров в магазине, то переменнаясчитается выходом системы:

. (5.5)

Таким образом, рассматриваемая система описывается уравнениями состояния (5.3) – (5.4) и уравнением выхода (5.5). Разностные уравнения состояния связывают значения переменных состояния ив последующий момент дискретного времениk + 1(следующий день) с переменными системы в текущий момент времениk. С использованием оператора сдвигаzполученые разностные уравнения (5.3) – (5.4) можно привести к операторной форме:

удобной для построения структурной схемы

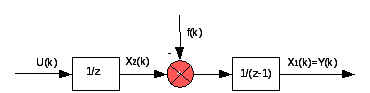
Рис. 5.2. Структурная схема склад – магазин

Модель дискретной системы может быть также представлена в форме вход – выход. Для этого уравнение (5.3) переписывается для времени k + 2:

После подстановки выражений (5.4) и (5.5), находим

Полученное разностное уравнение второго порядка связывает объемы товаров в моменты дискретного времени k+2 и k+1 с соответствующими значениями заказаu(k) и продаж f(k+1).

Для решения задачи стабилизации количества товаров в магазине yна заданном уровнеможет быть использована простейшая стратегия управления заказами – пропорциональный алгоритм управления

где - отклонение,К– постоянный коэффициент. Графики процессов в такой системе при постоянном спросеf(k) = constприведены на рисунках и представлены решетчатыми функциями:

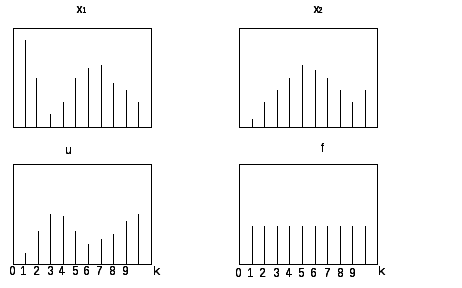
Рис. 5. 3. Процессы системы склад – магазин