7. Статические и астатические системы

Рассмотрим динамическую систему с одним входным воздействием x(t) [5]:

y(t) = W(p) x(t),

где

W(p) = A(p)/B(p),

А(p) = am p^m + am-1p+... +ao,

B(p) = bnpⁿ +bn-1 p+...+ b, .

Будем полагать, что в данном случае в качестве входа x(t)может выступать как задающее, так и возмущающее воздействие, а под системой управления подразумевается как разомкнутая система, так и замкнутая. Для статической системы, т.е. системы, у которойb0, значение передаточной функции в точкеp = 0определяется как :W(0) =a / b= k, гдеk– статический коэффициент системы, и при постоянном входном воздействиих(t) = constимеет место. Отметим, что для статической системы характеристическое уравнениеB(p) = 0не имеет нулевых корней. Включение статического (пропорционального) регулятора в схему управления уменьшает статизм замкнутой системы в1/(k+1)раз, гдеk– коэффициент усиления разомкнутой системы, при этом увеличивается астатизм, то есть возрастает точность выполнения командного (задающего) сигнала.

Теперь рассмотрим астатическую систему, полагая

b0= b1= …= bk-1= 0, bk0.

Ее характеристическое уравнение может быть приведено к виду

,

где

.

Такой полином имеет kнулевых корней. Числоkназвается порядком астатизма. Для астатической системы можно записать

,

где

.

Характерным признаком астатизма служит наличие в структурной схеме kинтегрирующих звеньев:

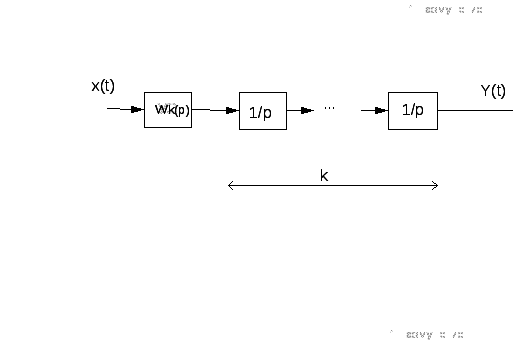
Порядок астатизма системы по управляющему воздействию равен числу интегрииующих звеньев, входящих в контур. Порядок астатизма замкнутой системы по отношению к рассматриваемому воздействию равен числу интегрирующих звеньев, включенных в цепь обратной связи между точками приложения этого воздействия (входом) и измерения ошибки (выходом) и не зависит от числа интегрирующих звеньев, включенных в цепь прямого преобразования сигнала между этими точками. Так как для астатической системы значение W(0)не определено, то можно ввести в рассмотрение показатель

,

называемый добротностью системы по соответствующей производной выходной переменной (по скорости, ускорению и т.д.). Отметим, что астатизм системы управления может быть обусловлен свойствами объекта управления или наличием в составе системы ПИиПИД– регуляторов. Реализация замкнутых систем с высоким порядком астатизма достаточно затруднительна, поскольку система автоматического регулирования, содержащая всего два интегрирующих звена, является структурно неустойчивой и не может быть реализована без специальных корректирующих устройств. Важно знать, что чем выше порядок астатизма системы, тем выше точность в установившемся режиме и меньше запас устойчивости. Введение пропорциональной составляющей в закон управления по отклонению влияет и на точность и на устойчивость.

В завершение раздела отметим следующие простые, но важные положения.

1. При любых последовательных и параллельных соединениях устойчивых систем всегда будет получаться устойчивая система.

2. Если среди соединяемых последовательно или параллельно систем имеется хотя бы одна неустойчивая, то и вся система, полученная в результате соединения, будет неустойчивой.

3. Исследование устойчивости любой линейной системы, полученной путем последовательного и параллельного соединения любого количества элементарных систем, может сводиться к исследованию устойчивости отдельных элементарных систем, входящих в ее состав.

4. Зная полюсы передаточных функций элементарных звеньев, легко определить какие полюсы в правой полуплоскости будет иметь передаточная функция системы, полученная путем последовательных и параллельных соединений этих звеньев, в случае, если она неустойчива.