3.1.6. Обобщенная теорема об эйлеровых цепях

Сформулируем еще одну теорему, являющуюся обобщением теоремы Эйлера.

Определение. Если граф является связным и имеет вершин нечетной степени, то в нем можно провести различных цепей, содержащих все его ребра в совокупности ровно по одному разу.

Доказательство. Обозначим нечетные вершины графа . Добавим к графу ребер . В новом графе все вершины четные, следовательно, должен существовать эйлеров цикл. Если теперь выбросить из найденного эйлерова цикла новые ребра, то цикл распадется на отдельных цепей, содержащих все ребра графа.

На методике доказательства может быть построен конструктивный алгоритм определения эйлеровых цепей на графе. Рассмотрим пример. Пусть задана схема трамвайных путей, которая может быть представлена графом на рис. 3.11. Требуется выбрать маршруты движения так, чтобы можно было добраться до любой точки схемы, делая пересадки лишь в точках, являющихся вершинами графа. Методика решения последовательно показана на рисунках 3.11a – 3.11d.

Рис. 3.11.

Пример. По шахматной доске ходит конь. Каждый его возможный ход может рассматриваться как связь между двумя клетками доски или как ребро графа, вершинами которого являются клетки доски. Можно ли проложить такой маршрут, чтобы конь сделал все ходы, не повторив ни одного из них дважды? Можно ли покрыть все клетки набором цепей, сколько их понадобится? Решить тот же пример для короля.

Для решения данной задачи нужно представить шахматную доску в виде графа, приписав каждой клетке локальную степень, равную числу различных ходов, которые может сделать из этой клетки конь. На рис. 3.12а представлена четверть шахматной доски. Число в клетке – количество различных ходов коня из этой клетки.

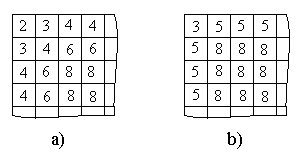
Рис. 3.12.

Из рис. 3.12a следует, что для коня граф имеет 8 вершин нечетной степени и, соответственно, не является эйлеровым. При этом граф имеет 8 вершин нечетной степени. Используя обобщенную теорему Эйлера, можно сделать вывод, что данный граф можно покрыть четырьмя эйлеровыми цепями.

Рис. 3.12b соответствует ходам шахматного короля. Построенный по этим данным граф также не является эйлеровым и может быть покрыт четырнадцатью эйлеровыми цепями.

Интересная и практически важная задача, имеющая смысл поиска эйлерова цикла на ориентированном графе, может быть сформулирована следующим образом: проложить маршрут осмотра экспонатов выставки, размещенных по обеим сторонам коридоров некоторого помещения. Очевидно, что данная задача имеет смысл поиска такого эйлерова пути на ориентированном графе, чтобы каждое ребро было пройдено дважды в разных направлениях. Разрешимость данной задачи определяется следующей теоремой.

Теорема. Чтобы в конечном ориентированном графе существовал эйлеров цикл, необходимо и достаточно равенство степеней вершин этого графа по входящим и выходящим дугам .

Учитывая, что любому н–графу канонически соответствует орграф, можно сформулировать следующее утверждение: в конечном связном н–графе всегда можно построить ориентированный цикл, проходящий через каждую дугу (проходящий через каждое ребро по одному разу в каждом из двух направлений).