3.1.5. Эйлеровы циклы и цепи

Эйлеров цикл – цикл, содержащий все ребра графа. Эйлеров граф – граф, имеющий эйлеров цикл.

Понятие эйлерова цикла связано с известной задачей Эйлера о Кенигсбергских мостах на реке Прегал. Схема этих мостов, соединяющих берега реки 2,3 с двумя ее островами 1,4 и острова между собой, приведена на рис. 3.8а. Эйлер сформулировал эту задачу следующим образом: можно ли, начав с некоторой точки, пройти все мосты по одному разу и вернуться в исходный пункт. Для решения задачи Эйлер преобразовал рисунок в граф, обозначив берега реки и острова как вершины графа, а мосты как ребра графа (рис. 3.8.b ).

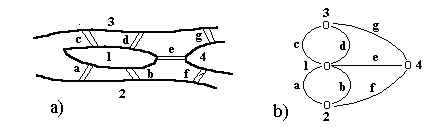
Рис. 3.8 Схема и граф для задачи о Кенигсбергских мостах.

Легко видеть, что в такой постановке задача о Кенигсбергских мостах эквивалентна задаче определения на графе такого цикла (циклического маршрута, не содержащего повторяющихся ребер), который проходит через все ребра графа. Ее решение дается следующей теоремой.

Теорема Эйлера: конечный неориентированный граф эйлеров тогда и только тогда, когда он связан и степени всех его вершин четны.

Необходимость этих условий достаточно очевидна. В несвязном графе каждый цикл принадлежит какой-либо его связной части, т.е. не проходит через все его части. С другой стороны, каждый раз, когда эйлеров цикл приходит в какую-либо вершину, он должен выйти из нее по другому ребру, т.е. инцидентные вершинам ребра можно разбить на пары соседних в эйлеровом цикле. Это относится и к начальной вершине, которая одновременно является и конечной. Для нее инцидентные ребра также распадаются на пары, но, кроме того, есть ребро, относящееся к началу цикла и ребро, относящееся к концу цикла.

Близкой по смыслу к задаче поиска эйлерова графа является так называемая задача графопостроителя. Она может быть сформулирована следующим образом: заданный плоский граф необходимо вычертить, не отрывая карандаша от бумаги и не обводя дважды одно и то же ребро.

Задача графопостроителя не эквивалентна задаче о Кенигсбергских мостах и допускает решение не только в классе эйлеровых циклов, так как не требует, чтобы головка графопостроителя возвращалась в исходную точку. Решение может лежать и в классе эйлеровых цепей.

Эйлерова цепь – цепь, включающая все ребра данного н–графа , но имеющая различные начальную и конечную вершины.

Теорема. Чтобы в конечном н–графе существовала эйлерова цепь, необходимы и достаточны его связность и четность степеней всех вершин, кроме начальной и конечной, которые должны иметь нечетные степени.

Рассмотрим некоторые примеры.

Пример. Схема и граф для задачи о Кенигсбергских мостах приведены на рис. 3.8.

В графе все вершины имеют нечетные степени. Следовательно, граф не имеет эйлерова цикла и решение поставленной задачи невозможно.

Пример. Имеют ли пятиугольник и пятигранник–пирамида, приведенные на рисунке 3.9, эйлеров цикл (цепь)?

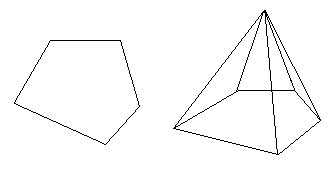
Рис. 3.9.

Локальная степень каждой вершины пятиугольника равна двум, т.е. четна. Соответственно, пятиугольник – эйлеров граф.

Пятигранник–пирамида имеет нечетные степени всех вершин и не является эйлеровым графом.

Пример. Найти эйлеров цикл для графа, представленного на рис. 3.10.

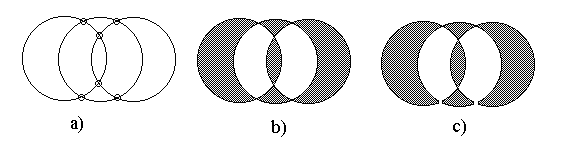
Рис. 3.10. Нахождение эйлерова цикла

Граф связный и имеет 6 вершин, все четные. Следовательно, данный граф – эйлеров и может быть нарисован одним росчерком пера. Откуда же начинать вычерчивание?

Существует следующий способ определения порядка вычерчивания: в графе следует выбрать одну область и заштриховать ее; область, граничащую с заштрихованной, пропустить, а имеющую лишь общую вершину заштриховать, и так действовать до тех пор, пока все возможные области не будут заштрихованы (рис. 3.10b).

Далее заштрихованный граф следует разъединить в одной или нескольких вершинах так, чтобы образовалась односвязная (без «дыр») заштрихованная область (рис.3.10с). Таким образом, теория графов дала не только условия разрешимости задачи, но и конструктивный метод ее решения.