2.4.6. Тупиковые днф

После того как сокращенная ДНФ построена, для получения минимальной ДНФ можно воспользоваться тривиальным алгоритмом. Ясно, что его эффективность будет еще выше. Возможен, однако, другой подход, связанный с перебором лишь так называемых тупиковых ДНФ.

Определение. Покрытие подмножества максимальными интервалами называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием.

Определение. ДНФ функции называется тупиковой, если ей соответствует неприводимое покрытие подмножества . Очевидно, что всякая минимальная ДНФ является тупиковой.

Пример. Рассмотрим функцию

и соответствующее ей подмножество (рис. 2.4.). Сокращенную ДНФ этой функции можно записать следующим образом: .

Т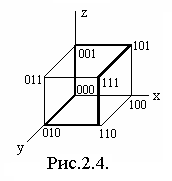упиковыми ДНФ являются:

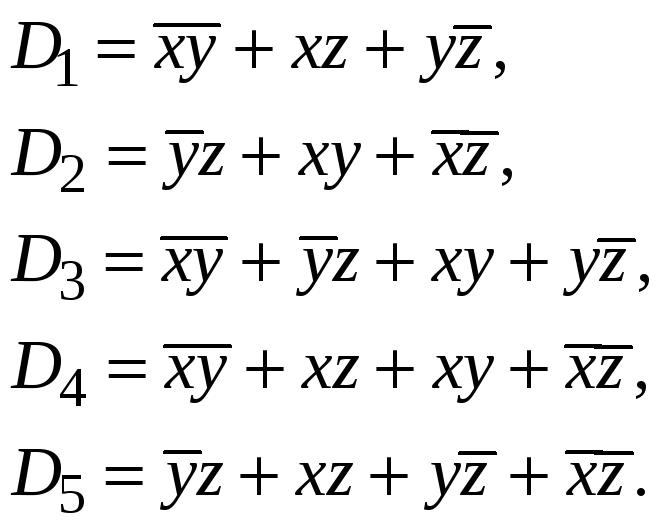
ДНФ являются минимальными для данной функции. ДНФ не являются минимальными. Таким образом, если сокращенная ДНФ строится однозначно, то процесс перехода от сокращенной ДНФ к тупиковой неоднозначен. Удаление одних элементарных конъюнкций из сокращенной ДНФ приводит к минимальной ДНФ, других – к тупиковой ДНФ, не являющейся минимальной. Поэтому, для построения минимальных ДНФ приходится строить все тупиковые ДНФ и среди них вести отбор. Процесс построения минимальных ДНФ на основе СДНФ или таблицы можно представить схемой, представленной на рис. 2.5.

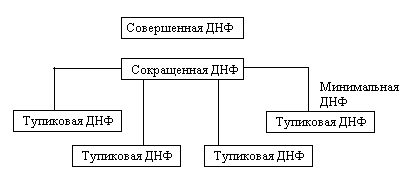
Рис. 2.5. Структура процесса построения минимальных ДНФ

Процедуру перехода от сокращенной ДНФ к тупиковой можно разбить на элементарные шаги, каждый из которых представляет собой удаление из ДНФ, полученной на предыдущем шаге, одной элементарной конъюнкции . Удаляемая конъюнкция такова, что 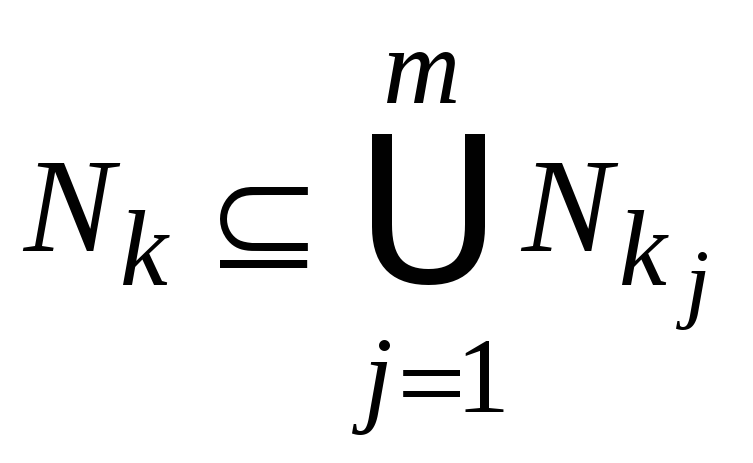, т.е. представляется суммой других интервалов. Для этого необходимо установить аналитический критерий покрытия некоторого интервала суммой других интервалов.

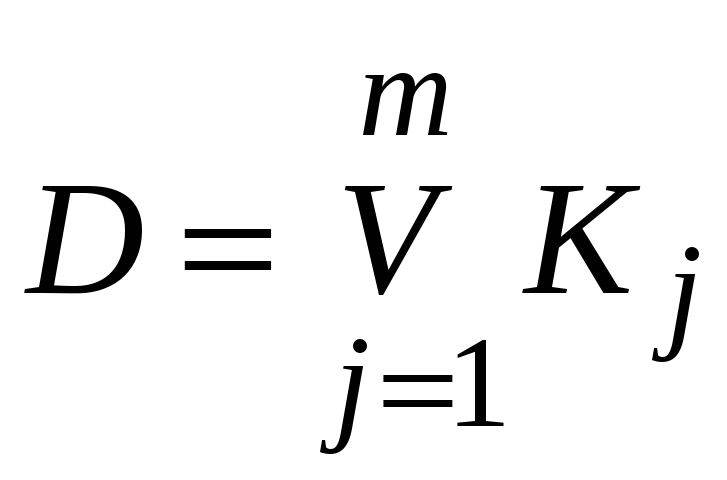Определение. Дизъюнкция элементарных конъюнкций поглощает элементарную конъюнкцию , если . Иначе, дизъюнкция поглощает конъюнкцию тогда и только тогда, когда .

Определение. Элементарные конъюнкции называются ортогональными, если .

Геометрический смысл ортогональных конъюнкций прост. Они соответствуют интервалам, не имеющим общих вершин. Для проверки ортогональности проще всего пользоваться следующим свойством: две элементарные конъюнкции ортогональны тогда и только тогда, когда есть переменная входящая в одну конъюнкцию с отрицанием, а во вторую – без отрицания.

Алгоритм проверки поглощения конъюнкции дизъюнкцией 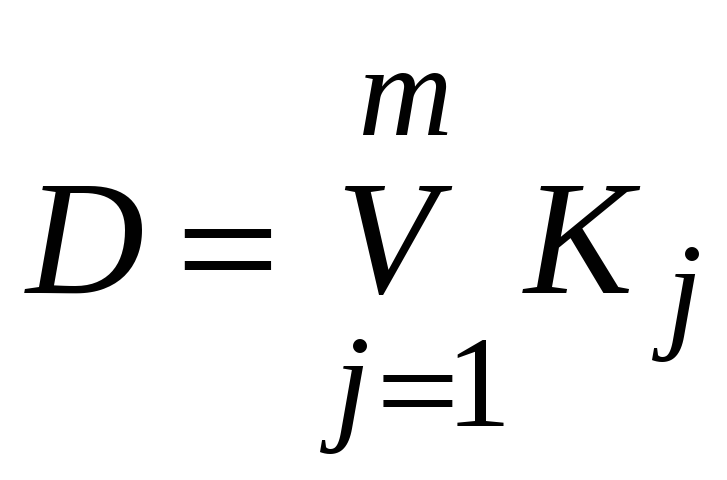включает следующие шаги:

• в дизъюнкции 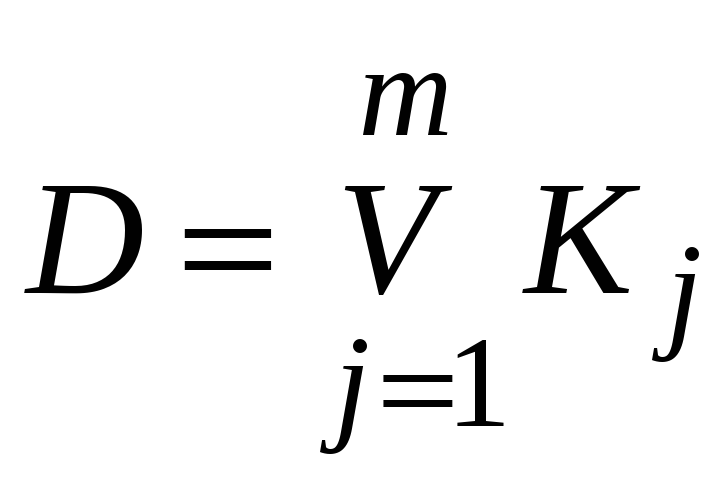выделяются конъюнкции неортогональные ;

• из всех выделенных конъюнкций удаляются термы , встречающиеся в ,

• выясняется, всегда ли равна 1 полученная после такого удаления дизъюнкция 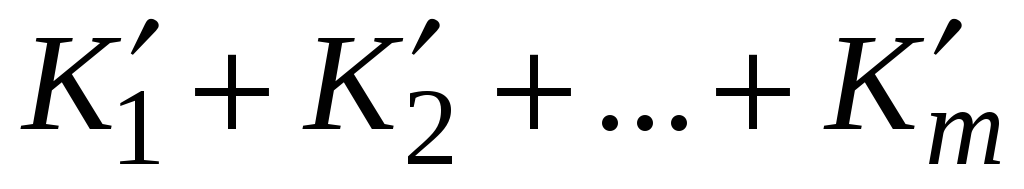. Если всегда, то конъюнкция поглощается дизъюнкцией и может быть вычеркнута из формулы.

Пример. Рассмотрим функцию из предыдущего примера. Сокращенная ДНФ имеет вид .

Выделим конъюнкцию и все неортогональные к ней конъюнкции: . Проверим выполнение условия . Для этого удаляем из термы . Получаем дизъюнкцию , тождественно равную 1. Таким образом, конъюнкция поглощается дизъюнкцией и ее можно удалить из . В результате имеем .

Во вновь полученной дизъюнкции выделим конъюнкцию и все неортогональные к ней конъюнкции: . Удаляем из термы и . Получаем . Конъюнкцию можно удалить из . В результате имеем .

Полученная формула является тупиковой. Это несложно установить, проверив условия поглощения для каждой из оставшихся в конъюнкций. Рассмотрим, например, конъюнкцию . Неортогональна к ней только конъюнкция . Однако условие не является тождеством и, следовательно, не поглощается .

Другой вариант состоит в последовательном исключении конъюнкций . Такая последовательность операций ведет к форме , которая является минимальной.