2.1.4. Функционально полные системы (базисы)

Важной задачей математической логики являются преобразования логических формул. Эквивалентными или равносильными называют формулы, представляющие одну и ту же функцию. Стандартный метод установления эквивалентности двух формул состоит в следующем:

• по каждой формуле восстанавливается таблица истинности;

• полученные таблицы сравниваются по каждому набору значений переменных;

• если на всех наборах формулы дают одинаковые истинностные значения, они эквивалентны.

Пример: доказать эквивалентность формул .

Воспользуемся стандартным методом, т.е. построим таблицу истинности для всех трех формул.

Таблица 2.4.

00	1	0	1	1	1	1
01	1	0	1	1	0	1
10	1	0	1	0	1	1
11	0	1	0	0	0	0

Полученные результаты говорят о том, что формулы эквивалентны.

Как видно из примера, одна и та же логическая функция может быть задана формулами, включающими различные наборы логических операций. Существуют наборы логических операций, с помощью которых можно выразить любые другие логические операции. Такие наборы называются функционально полными системами, или базисами. Примерами таких базисов логических операций являются: , .

Наиболее хорошо изученным является базис . Формулы, содержащие только операции конъюнкции, дизъюнкции и отрицания называются булевыми. Следующие две теоремы, приведенные без доказательств, устанавливают правила перехода от одного базиса к другому.

Теорема 1

Всякая логическая формула может быть представлена булевой формулой.

Теорема 2

Если все функции функционально полной системы представимы формулами над , то также функционально полна.

Таким образом, чтобы перейти в записи логической формулы от одного базиса к другому, нужно просто заменить все операции первого базиса через операции второго базиса.

Алгебра , основным множеством которой является множество всех логических функций , а операциями (т.е. сигнатурой ) – конъюнкция, дизъюнкция и отрицание, называется булевой алгеброй логических функций.

2.1.5. Совершенная дизъюнктивная нормальная форма

Система операций булевой алгебры полна и переход от табличного задания любой логической функции к формуле булевой алгебры, всегда возможен. Сформулируем очень важный для практики способ перехода от табличного задания логической функции к булевой формуле. Он включает следующие действия:

• для каждого набора значений переменных 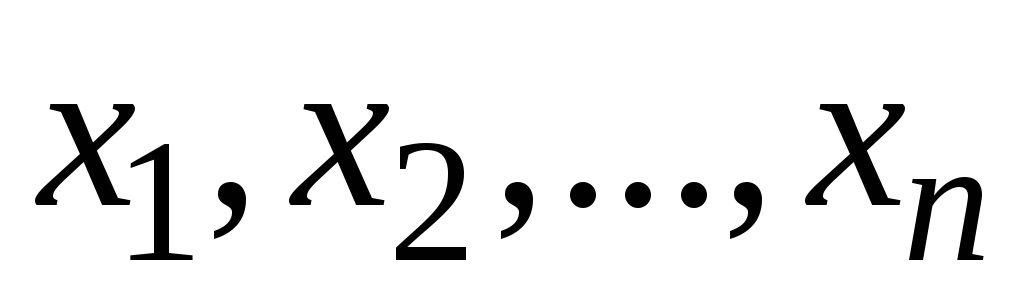, на котором функция равна 1, выписываются конъюнкции всех переменных;

• над теми переменными, которые на этом наборе равны 0, ставятся отрицания;

• все такие конъюнкции соединяются знаками дизъюнкции.

Полученная таким образом формула называется совершенной дизъюнктивной нормальной формой (СДНФ) логической функции. Для каждой функции СДНФ единствена.

Пример: для логической функции, заданной в таблице 2.3, СДНФ имеет вид

.

Переход от логической формулы произвольного вида, или формулы записанной в некоторой не булевой алгебре с сигнатурой возможен не только через таблицу истинности, но и на основе теоремы 2. Для этого необходимо лишь выразить элементы через дизъюнкцию, конъюнкцию и отрицание.

Пример. Перевести в булев базис следующую логическую формулу .

Для решения задачи воспользуемся соотношением , правильность которого легко проверить через построение таблицы истинности. Последовательно проводя преобразования будем получать

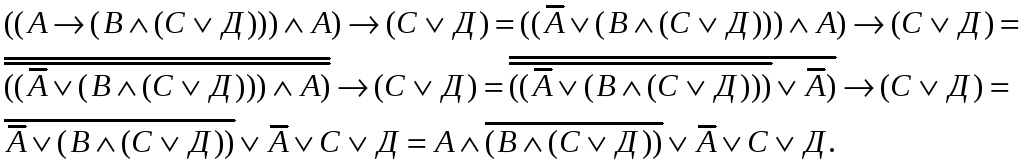
Пример. В алгебре Жигалкина , ее сигнатура является функционально полной системой. Убедиться в этом, используя теоремы 1 и 2.

Решение. Из теоремы 1 следует, что набор булевых функций полон. Тогда, в соответствии с теоремой 2, для доказательства функциональной полноты набора достаточно доказать следующие равенства:

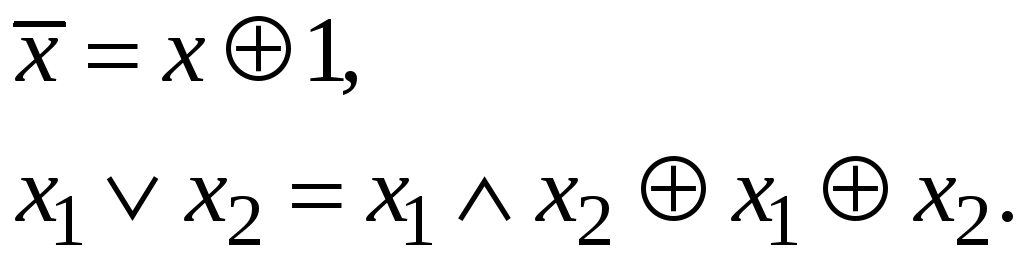
Используя обычный подход, построим таблицы истинности 2.5 и 2.6.

Таблица 2.5.

x		1	x1
0 1	1 0	1 1	1 0

Таблица 2.6.

0 1 0 1 1	0 1 1 1	0 0 0 1	0 0 1 0	0 1 1 1

Из полученных таблиц истинности следует, что алгебра Жигалкина функционально полна.