2.1.6. Основные эквивалентные соотношения в булевой алгебре

1. Ассоциативность конъюнкции и дизъюнкции:

,

.

2. Коммутативность конъюнкции и дизъюнкции:

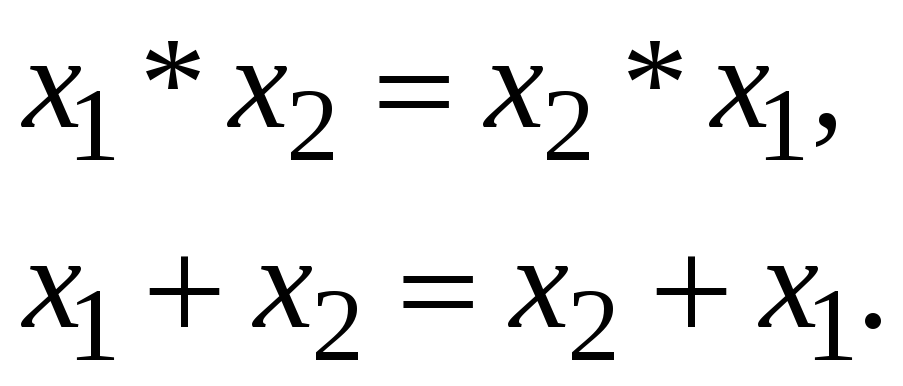
3. Дистрибутивность конъюнкции относительно дизъюнкции:

.

4. Дистрибутивность дизъюнкции относительно конъюнкции:

.

5. Идемпотентность:

6. Закон двойного отрицания: .

7. Свойства констант 0 и 1:

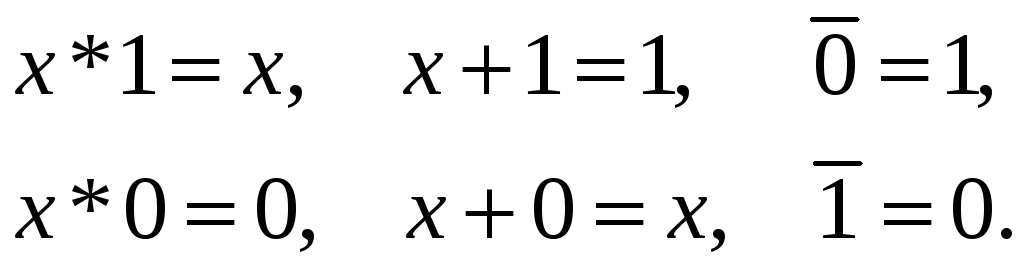
8. Правила де Моргана

, .

9. Закон противоречия: .

10. Закон исключенного третьего .

Особенность данных эквивалентных соотношений в том, что:

• они не выводимы друг из друга. Убедиться в их справедливости можно путем построения таблиц истинности;

• этих соотношений достаточно для выполнения любых эквивалентных преобразований.

Кроме основных соотношений часто используются следующие соотношения, выводимые из основных:

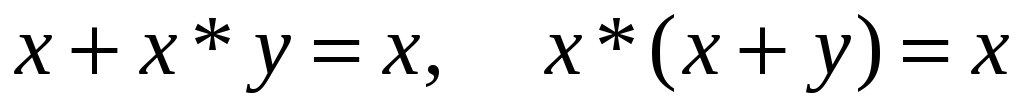• (поглощение),

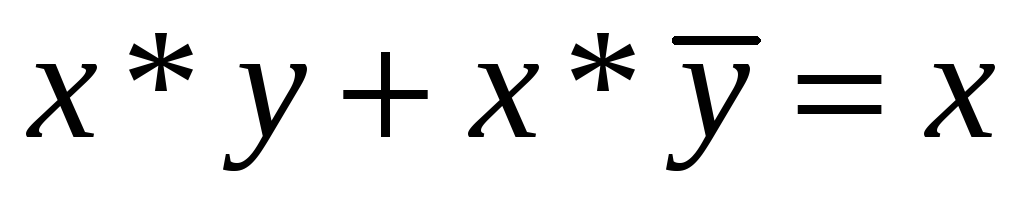• ( склеивание),

• .

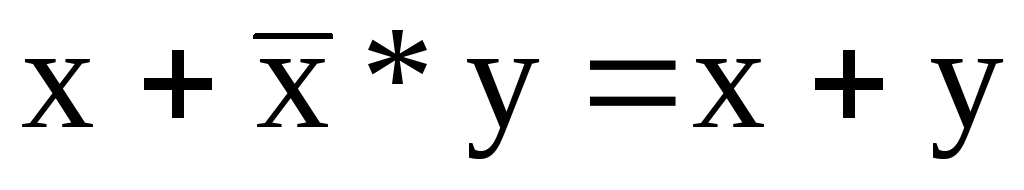На основе основных и дополнительных эквивалентных соотношений булевой алгебры возможно проведение преобразований логических формул с целью получения более простых выражений.

Примеры.

1. Упростить булеву формулу .

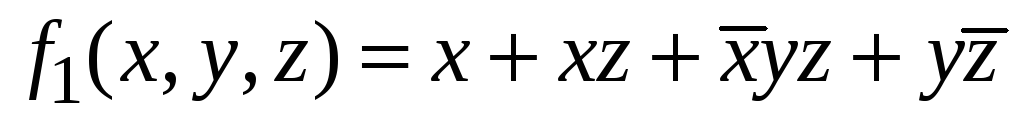Решение : .

2. Упростить булеву формулу .

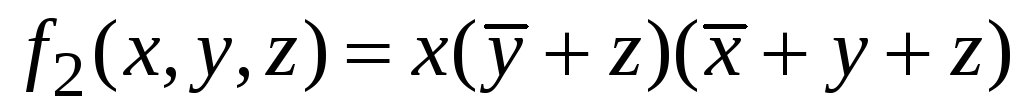Решение : .

2.1.7. Переход от днф к сднф методом расщепления

Иногда возникает задача восстановления для логической функции, описываемой ДНФ произвольного вида к совершенной дизъюнктивной нормальной форме, реализующей ту же логическую функцию. Этот переход возможен, конечно, через таблицу истинности, однако более простым является так называемый мотод расщепления. Рассмотрим его на примере. Пусть логическая функция трех переменных представлена следующей логической формулой

.

Переход к СДНФ проведем путем следующих очевидных преобразований

.

2.2. Формы представления булевых функций

Выше рассмотрены две формы представления булевых функций – таблицы истинности и логические формулы. Познакомимся с некоторыми другими формами.

2.2.1. Геометрическое представление булевых функций

В геометрическом смысле каждый набор значений переменных можно рассматривать как – мерный вектор, определяющий точку в –мерном пространстве. Все множество двоичных наборов значений аргументов образует геометрическое множество вершин –мерного единичного куба. Выделяя вершины, на которых значение функции равно 1, можно получить геометрический образ истинностной функции.

Пример. Функция задана таблицей истинности 2.7. Геометрическим представлением ее области истинности являются вершины куба, отмеченные на рис. 2.2 черными точками.

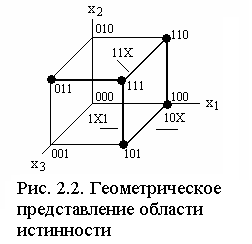Таблица 2.7.

	f()
000 001 010 011 100 101 110 111	0 0 0 1 1 1 1 1

Расстоянием между двумя вершинами называется число переменных, значения которых следует изменить, чтобы преобразовать вектор координат одной вершины в вектор координат другой.

2.2.2. Интервальное представление булевых функций

Интервальное представление устанавливает более тесную связь между геометрическим представлением логической функции и ее записью в виде логической формулы в булевом базисе. Обозначим – множество всех вершин единичного n –мерного куба. Пусть – множество всех таких вершин куба, на которых функция . Для вышеприведенного примера . Множество является, фактически, отношением на вида .

Сформулированное в разделе 2.1.5 правило получения СДНФ связывает с каждой вершиной n –мерного куба конъюнкцию членов, а со всей областью истинности функции – дизъюнкцию этих конъюнкций. Пусть для некоторой функции . Тогда СДНФ имеет вид . Применив к полученной формуле операцию склеивания по получим . Легко заметить, что исходные вершины соединены ребром. Если связать с этим ребром конъюнкцию , то можно построить цепочку: конъюнкция трех составляющих – вершина куба, конъюнкция двух составляющих – ребро куба и т.д.

Для формализации полученной связи между конъюнкциями и элементами гиперкуба введем несколько определений.

Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний , где 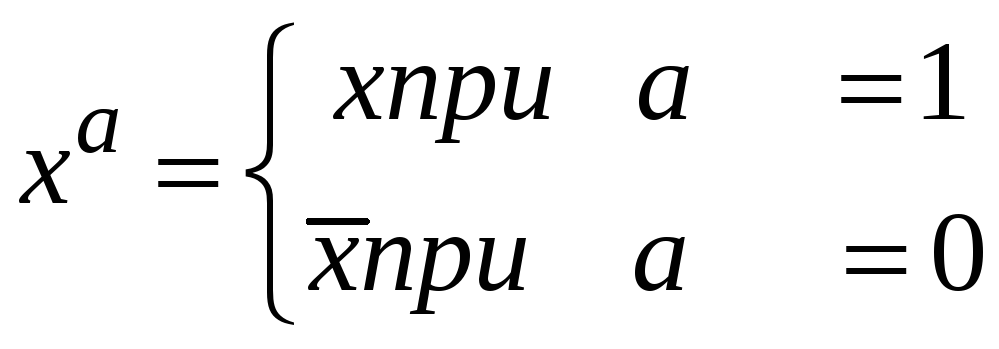, в которой каждая переменная встречается не более одного раза. Часто, в литературе, переменную или ее отрицание вида называют первичным термом. Число называется рангом конъюнкции. В случае конъюнкция называется пустой и полагается равной 1.

Подмножество называется интервалом r–ого ранга, если оно соответствует элементарной конъюнкции –ого ранга.

Очевидно, каждой конъюнкции соответствует интервал , состоящий из всех вершин гиперкуба, у которых а значения остальных координат произвольны. Таким образом, каждая вершина куба является интервалом –ого ранга, множество всех вершин – интервалом нулевого ранга.

Пример. В трехмерном кубе, конъюнкции соответствует ребро , являющееся интервалом 2–го ранга (такой интервал часто обозначают (X11)), а конъюнкции – грань , являющаяся интервалом 1–го ранга.

Для некоторой логической функции можно ввести понятие комплекса интервалов –ого ранга. Например, для функции, заданной выше таблицей истинности 2.7 и рисунком 2.2, можно выделить следующие комплексы: