3.3.2. Вывод в четырехзначной диалоговой логике Ldmin

В предыдущем параграфе введена и описана четырехзначная диалоговая логика L_dmin, рассмотрены операции отрицания, конъюнкции, дизъюнкции, импликации и выявлены их свойства, также доказано, что система операций {¬₂,¬₃,₁} образует базис данной логики. Однако, этого недостаточно для практического применения, необходим эффективный механизм вывода и, в первую очередь, определения общезначимости формулы в логике L_dmin.

Проверять общезначимость можно различными способами, например, наиболее просто способ проверки заключается в использовании простого перебора. Очевидно, это не самый оптимальный способ. В качестве альтернативы используем метод, основанный на аналитических таблицах.

Для начала введём следующие определения.

Определение 3.14. Пусть X есть конечное множество атомарных формул X = {a, b, c …}, тогда однозначное соответствие s: XL_dmin называется сетапом, или единичным сетапом, здесь L_min = {T,F,I,E}.

Определение 3.15. Формула F является выполнимой в логике L_dmin, если существует такой сетап s, при котором F принимает значение T.

Определение 3.16. Формула F является общезначимой в логике L_dmin, если на любом сетапе s, F принимает значение T.

Определение 3.17. Формула F является внутренне выполнимой в логике L_dmin, если существует такой сетап s, при котором F принимает значение T или I.

Определение 3.18. Формула F является внутренне общезначимой в логике L_dmin, если на любом сетапе s, F принимает значение T или I.

Определение 3.19. Формула F является внешне выполнимой в логике L_dmin, если существует такой сетап s, при котором F принимает значение T или E.

Определение 3.20. Формула F является внешне общезначимой в логике L_dmin, если на любом сетапе s, F принимает значение T или E.

Очевидно, что формула общезначима тогда и только тогда, когда она общезначима и внутренне и внешне. Однако, и внешняя и внутренняя выполнимость формулы не гарантируют ее общую выполнимость.

Существует два варианта вывода на базе аналитических таблиц: с использованием означенных формул и без них. В диссертации используется вариант с использованием означенных формул.

Определение 3.21. Означенная формула – это запись вида FX, TX, IX или EX, где X - формула.

В классическом методе аналитических таблиц TX читается как “X – истина”, а FX “X – ложь”. Аналитическая таблица – это дерево с означенными формулами в качестве подписей в узлах дерева. В корне дерева находится исходная означенная формула. Ветви дерева получаются декомпозицией формулы, выполняемой по определенным правилам.

В классической логике если формула X выводима (общезначима), то она не может быть ложью. При доказательстве формулы табличным способом первоначально формула X отвергается. Для того, чтобы доказать некоторую формулу X, ей приписывается ложное значение (FX), после чего строится дерева вывода для FX с целью получить противоречие. Если противоречие получено, формула X считается доказанной. Критерием противоречия является замкнутость дерева вывода. Ветвь дерева называется замкнутой, если она содержит одновременно FA и TA, где A – некоторая подформула исходной формулы X. Если все ветви дерева формулы FX являются замкнутыми, то дерево вывода является замкнутым.

В методе аналитических таблиц для классической логики применяются следующие правила построения подветок: если встречается T(XY), то образуется два новых элемента ветви TX и TY. В случае, если встречается F(XY), ветвь расщепляется на две, в одной из которых добавляется FX, в другой FY.

При построении метода вывода на базе аналитических таблиц для четырехзначных логик важно определить способ означивания формул и дать критерий замкнутости дерева вывода.

Определение 3.22. Дерево вывода означенной формулы X, это граф (G,V) связностью 1, каждая вершина которого помечена означенной формулой, таким образом, что потомками каждой вершины являются вершины, помеченные формулами получающимися при декомпозиции означенной формулы, находящийся в вершине дерева.

Означенная формула Y является декомпозицией означенной формулы Х, YX, тогда и только тогда когда получена из Х при помощи правил декомпозиции. Существует четыре типа правил: -правила, -правила, -правила и -правила аналогичные правилам для логики Белнапа, предложенным Фиттингом (см.[140]).

								
1		1		1	3	4		1	3	5	6
		2		2	1	2		2	4

	1			1			1	2
T¬2X	TX		T4X	IX		F X1Y	FX	FY
I¬2X	EX		I4X	TX
E¬2X	IX		E4X	FX
F¬2X	FX		F4X	EX

	1	2	3	4
I X1Y	IX	IY	FY	FX
E X1Y	EX	EY	FY	FX

	1	2	3	4	5	6
T X1Y	IX	EY	EX	IY	TX	TY

Рис 3.3. Правила декомпозиции базисных функций в логике L_dmin

Так как операции {¬₂, ₄,₁} образуют базис в L_dmin, то набор приведенных выше правил достаточен для декомпозиции произвольной формулы L_dmin. Для удобства использования можно аналогичным образом построить правила вывода для производных операций (см. рис 3.4).

	1			1			1	2
T1X	FX		T5X	EX		T X1Y	TX	TY
I1X	EX		I5X	FX		E X2Y	EX	EY
E1X	IX		E5X	TX		I X2Y	IX	IY
F1X	TX		F5X	IX		F X1Y	TX	FY

	1	2	3	4
I X1Y	IX	IY	TY	TX
E X1Y	EX	EY	TY	TX
T X2Y	TX	TY	EY	EX
F X2Y	FX	FY	EY	EX
T X2Y	TX	TY	IY	IX
F X2Y	FX	FY	IY	IX
E X1Y	IX	EY	FY	TX
I X1Y	EX	IY	FY	TX

	1	2	3	4	5	6
F X1Y	IX	EY	EX	IY	FX	FY
I X2Y	TX	FY	FX	TY	IX	IY
E X2Y	TX	FY	FX	TY	EX	EY
T X1Y	IX	IY	EX	EY	FX	TY

Рис 3.4. Правила декомпозиции производных функций в логике L_dmin

Определим отношение декомпозиции .

Пусть x и y – ППФ L_dmin, тогда xy тогда и только тогда когда:

или x соответствует , y соответствует ₁, в -правиле,

или x соответствует , y соответствует ₁, в -правиле,

или x соответствует ₁, y соответствует ₂, в -правиле,

или x соответствует , y соответствует ₁, в -правиле,

или x соответствует , y соответствует ₃, в -правиле,

или x соответствует , y соответствует ₄, в -правиле,

или x соответствует ₁, y соответствует ₂, в -правиле,

или x соответствует ₃, y соответствует ₁, в -правиле,

или x соответствует ₄, y соответствует ₂, в -правиле.

Лемма 3.4 Для любой ППФ L_dmin существует дерево вывода.

Доказательство. Существует единственное правило декомпозиции (см. 3.3) для любой связки из множества {¬₂, ₄,₁} и любого значения формулы, т.е. для любой означенной формулы вида D¬₂F₁, D₄F₁, DF₁₁F₂, где D{T,F,E,I}, F₁,F₂ППФ L_dmin, существует единственное правило декомпозиции, применив которое мы уменьшаем количество логических связок на 1, в конечном итоге неизбежно перейдем к атомарным формулам, которые не могут быть далее разложены по правилам декомпозиции, но которые выражают ограничения на значение соответствующих переменных.

Определение 3.23. Ветвь дерева вывода называется замкнутой, если в ней существуют две вершины, помеченные одинаковыми формулами, означенными различным образом.

Определение 3.24. Дерево вывода означенной формулы X, является замкнутым тогда и только тогда, когда каждая его ветвь замкнута.

Ветвь дерева вывода означенной формулы DX означает набор значений, которые должны принимать подформулы, чтобы формула принимала указанное значение. Причем, если из одной вершины выходит несколько ветвей, это означает, что возможны различные наборы значений подформул. Замкнутость ветви означает противоречивость требований, накладываемых на некоторую подформулу, которая должна одновременно принимать несколько различных значений. Замкнутость дерева вывода означенной формулы DX означает невозможность формулы принимать значение D.

В связи с этим, для определения возможных значений формулы необходимо построить деревья вывода для всех вариантов означивания и определить их замкнутость.

Таблица 3.10. Результаты вывода для формулы Х методом аналитических таблиц.

TX	FX	IX	EX	Результат
не замкнуто	замкнуто	замкнуто	замкнуто	Х тождественно истинно (всегда принимает значение T)
замкнуто	не замкнуто	замкнуто	замкнуто	Х тождественно ложно (всегда принимает значение F)
замкнуто	замкнуто	не замкнуто	замкнуто	Х тождественно внутренне истинно (всегда принимает значение I)
замкнуто	замкнуто	замкнуто	не замкнуто	Х тождественно внешне истинно (всегда принимает значение E)
не замкнуто	не замкнуто	замкнуто	замкнуто	Х тождественно согласно (всегда принимает значение T или F)
замкнуто	замкнуто	не замкнуто	не замкнуто	Х тождественно спорно (всегда принимает значение I или E)
не замкнуто	замкнуто	не замкнуто	замкнуто	Х тождественно истинно для первого агента (всегда принимает значение T или I)
не замкнуто	замкнуто	замкнуто	не замкнуто	Х тождественно истинно для второго агента (всегда принимает значение T или E)
замкнуто	не замкнуто	замкнуто	не замкнуто	Х тождественно ложно для первого агента (всегда принимает значение F или E)
замкнуто	не замкнуто	не замкнуто	замкнуто	Х тождественно ложно для второго агента (всегда принимает значение F или I)
не замкнуто	не замкнуто	не замкнуто	не замкнуто	Х полностью неопределенно (может принимать любые значения)
замкнуто	не замкнуто	не замкнуто	не замкнуто	Х частично неопределенно (X не может принимать значение T)
не замкнуто	замкнуто	не замкнуто	не замкнуто	Х частично неопределенно (X не может принимать значение F)
не замкнуто	не замкнуто	замкнуто	не замкнуто	Х частично неопределенно (X не может принимать значение I)
не замкнуто	не замкнуто	не замкнуто	замкнуто	Х частично неопределенно (X не может принимать значение E)

Приведем пример вывода при помощи аналитических таблиц в L_dmin. Пусть дана формула é₄A Ú₁¬₂é₄¬₂A, докажем что она является тавтологией.

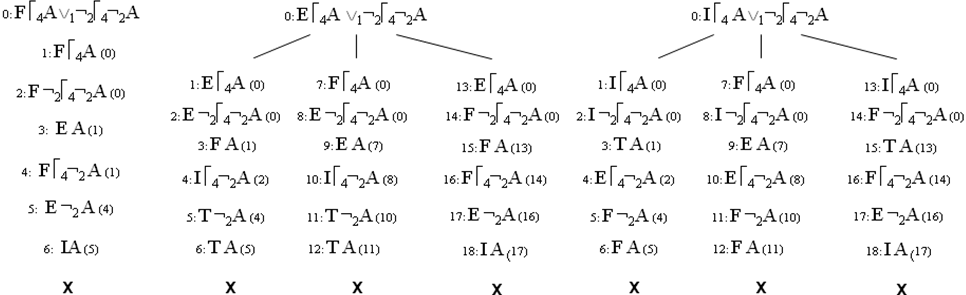
Рис 3.5. Пример вывода при помощи аналитических таблиц в L_dmin.

Как видим на рис 3.5, все деревья для означиваний F, E и I являются замкнутыми. Следовательно, формула é₄A Ú₁¬₂é₄¬₂A может принимать только значение T, т.е. é₄A Ú₁¬₂é₄¬₂A – тождественно истинна.