3.3. Базовые логики для описания диалогов между агентами

3.3.1. Минимальнозначная логика диалога

Как известно, семантика логики вопросов и ответов Белнапа иллюстрируется с помощью логической решетки L4, задающей порядок истинности _V, а семантика логики Фитинга – с помощью аппроксимационной решетки Скотта A4, порядок которой отождествляется с порядком знаний _К. В [100] были введены модальные решетки M4 и М4, опирающиеся на порядок уверенности (необходимости) и порядок предположения (возможности). Ниже по аналогии введем понятия диалоговой решетки и двойственной ей решетки диспута (или конкурентной решетки).

Вначале построим минимальнозначную диалоговую логику L_dmin на основе произведений двузначных логик двух агентов 1 и 2 – участников диалога. Множество логических значений можно представить графически в виде диалоговой решетки D4, представленной следующей диаграммой Хассе (рис 3.1).

Рис. 3.1. Диаграмма Хассе для диалоговой решётки D4.

Четырёхзначная семантика диалога L_dmin строится как произведение семантик агентов – участников диалога. Интерпретация полученных истинностных значений интуитивно вполне понятна: <F₁,F₂> – «ложь для обоих агентов», <T₁,F₂> – «истина для первого агента, ложь для второго», <F₁,T₂> – «ложь для первого агента, истина для второго», <Т₁,T₂> – «истина для обоих агентов». Здесь пары <F₁,F₂>, <T₁,T₂> можно понимать как точки согласия, а пары <T₁,F₂>, <F₁,T₂> как точки противоречия.

Если цель диалога формулируется как достижение соглашения, то соответствующее отношение порядка можно понимать как порядок cоглашения _С. Например, <F₁,F₂> _С <T₁,F₂> _С <Т₁,T₂> означает, что ситуация «истина для обоих агентов», равнозначная наличию соглашения между ними, будет предпочтительнее ситуации «истина одного агента – ложь другого», когда соглашения между агентами нет, но оно считается возможным. Последняя ситуация предпочтительнее, чем «ложь для обоих агентов», которая здесь отождествляется с невозможностью заключения соглашения (или отказом от него). Итак, в логике соглашения выделенным значением является <Т₁,T₂> = T (cм. таблицу 3.1).

Таблица 3.1. Истинностные значения четырёхзначной диалоговой логики

Значение в бирешетке D4	Обозначение	Интерпретация
<T1,T2>	T	Подтвержденная (согласованная) истина
<T1,F2>	I	Внутренняя истина (истина для первого агента)
<F1,T2>	E	Внешняя истина (истина для второго агента)
<F1,F2>	F	Подтвержденная ложь

Данная логика предназначена для согласования мнений агентов в процессе диалога, т.е. соответствует диалогам убеждения.

В свою очередь, повернув диалоговую решётку D4 по часовой стрелке на 90 градусов, получаем решётку диспута (спора) K4 с отношением порядка _G (порядок выигрыша). Здесь можно использовать аргументационную семантику, например, T – «аргумент найден», а F – «возражение не найдено». При этом <T₁,F₂> интерпретируется как победа в споре первого агента и поражение второго, поскольку первый агент нашел неопровержимый аргумент, <F₁,T₂> – как обратная ситуация, <Т₁,T₂> – как ничья (аргументы обоих агентов взаимно опровергаемы), а <F₁,F₂> – как отказ от спора. Тогда, например, имеем <F₁,T₂> _G <F₁,F₂> _G ,<T₁,F₂>, т.е. в логике диспута K₄ значение <T₁,F₂> следует брать в качестве выделенного значения.

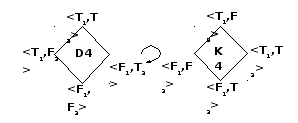
Рис. 3.2. Переход от диалоговой решётки D4 к решётке диспута K4

На основе решёток D4 и K4 легко построить диалоговую бирешётку. Пусть V, _С,_G  – биупорядоченное множество. В случае, когда его компоненты V, _С и V,_G  образуют полные решетки, биупорядоченное множество превращается в предбирешётку. Наконец, получаем диалоговую бирешётку, когда два различных отношения порядка связаны между собой с помощью специальной операции операции отрицания ¬₂, удовлетворяющей условиям:

v₁,v₂V, v₁_Сv₂  ¬₂v₂_С¬₂v₁; (3.1)

v₁,v₂V, v₁_Gv₂  ¬₂v₁_G¬₂v₂; (3.2)

vV, ¬₂¬₂v=v. (3.3)

Рассмотрим операции логики L_dmin. Общее количество возможных унарных операций в логике L_dmin равно 4⁴=256, бинарных (4⁴)²=65536. Если предположить, что T соответствует бинарной истине, а F - бинарной лжи, то можно определить консервативное отрицание. Унарная операция n является операцией консервативного отрицания в том случае, если n(T)=F, а n(F) = (T). Таких операций 16. Инверсивным отрицанием назовем такую унарную операцию n, которая меняет порядок истинности: x≥₁y  n(y)≥₁n(x), таких отрицаний насчитывается 36, из них 32 консервативных. Если же требовать x>₁y  n(y)>₁n(x), то есть строгой инверсивности, то таких отрицаний будет всего 12 (из них все консервативные). Отрицание n является биективным, если существует обратная операция n^-1, такая что n(n^-1(x))=n^-1(n(x))=x. Если n^-1=n, то такое отрицание назовем классическим (выполняется закон снятия двойного отрицания).

Однако наибольший интерес с точки зрения интерпретации вызывают, по мнению автора, следующие классические отрицания.

Таблица 3.2. Отрицания в логике L_dmin

x	ù1x	Ø2 x	Ø3 x	é4 x	é5 x
T	F	T	F	E	I
I	E	E	I	F	T
E	I	I	E	T	F
F	T	F	T	I	E

Первое отрицание ₁x, являющееся примером составного, однородного, консервативного отрицания, представляет собой обращение (инверсию) обоих базовых порядков _С и _G. Так отрицание по порядку _С показывает, что противоположностью соглашения между агентами T является невозможность его заключения F, тогда как отрицание по порядку _G означает конверсию – смену ролей агентов (пропонент превращается в оппонента, первоначальный победитель оказывается побежденным и т.п.).

Следующие два отрицания являются примерами составных неоднородных отрицаний. Так второе отрицание ¬₂, совпадающее по форме с отрицанием Фиттинга, сохраняет порядок соглашения _С, но инвертирует порядок диспута _G (показывая, например, смену ролей агентов). Подобная конверсия может применяться при рефлексивных рассуждениях.

В свою очередь, третье отрицание ¬₃, которое инвертирует порядок соглашения _С, но сохраняет порядок диспута _G, аналогично отрицанию Белнапа: противоположностью соглашения оказывается отказ от него (свойство консервативности), в то время как порядок диспута не меняется. По сути, в данном случае диалог агентов «заходит в тупик».

Операции отрицания позволяют естествнным образом представить возражения агентов друг другу. Так четвёртое отрицание ₄ семантически соответствует возражению оппонента пропоненту (внутреннее возражение в случае рефлексивных рассуждений), а пятое отрицание ₅. – возражению пропонента оппоненту. В совокупности отрицания ₄ и ₅ формируют операцию циклического отрицания.

Рассмотрим свойства введённых операций:

₁₁х = ¬₂¬₂х = ¬₃¬₃х = ₄ ₄ х = ₅ ₅ х = х (3.4)

₁х = ₄ ₅ х (3.5)

₄ х = ¬₂ ₅ ¬₂х , ₅ х = ¬₂ ₄ ¬₂х (3.6)

₁¬₂х = ¬₂₁х, ₁₄х = ₄₁х, ₁₅х = ₅₁х, ₄₅х = ₅₄х, (3.7)

Обратим внимание на то, что отрицания ¬₂ и _4, ¬₂ и _5, ¬₃ и _4, а также ¬₃ и ₅ не перестановочны, т.е.

¬₂₄х  ₄¬₂х, ¬₂₅х  ₅¬₂х, ¬₃₄х  ₄¬₃х, ¬₃₅х  ₅¬₃х, (3.8)

Лемма 3.1 Композиция унарных операций отрицания {₄,₅} и любой нульарной (константной) операции {F,E,I,T} позволяют построить любую нульарную функцию над L_dmin.

Доказательство. Рассмотрим два произвольных значения x, y  L_dmin.

Пусть x = (x₁,x₂), y = (y₁,y₂). Требуется доказать, что существует последовательность _i1 _i2… _iN , такая что _i1 _i2… _iNx = y. Рассмотрим 4 случая:

x₁ = y₁ и x₂ = y₂, тогда x = y

x₁  y₁ и x₂ = y₂, тогда ₄x = y

x₁  y₁ и x₂  y₂, тогда ₄₅x = y

x₁ = y₁ и x₂  y₂, тогда ₅x = y.

Если при произвольном =x мы получаем любой требуемый нам у, т.е. произвольную нульарную функцию. Лемма доказана.

Другие подобные системы операций вытекают из соотношений (3.5), (3.6). Этими системами отрицаний являются: {,¬₂,₄}, {,¬₂,₅}, {,¬₃,₄}, {,¬₃,₅}, {,¬₁, ₄}, {,¬₁, ₅}. Системы {,₁,¬₂}, {,₁,¬₃} и {,¬₂,¬₃} не являются полными, так как в силу своей рефлексивной симметричности, операции ₁, ¬₂ и ¬₃ не могут превратить точку согласия в точку противоречия и наоборот. Очевидно, что ни одна из операций ₃ ₄ также не может являться достаточной, поэтому {₄,₅}, {¬₂,₄}, {¬₂,₅}, {¬₃,₄}, {¬₃,₅}, {₁,₄}, {₁,₅} минимальные системы отрицаний.

Рассмотрим теперь правила композиции. Логические операции «или» и «и» определим, как взятие наименьшей верхней и наибольшей нижней грани частичных порядков _С и _G.

Таблица 3.3. Истинностная конъюнкция в логике L_dmin

x1y	T	I	E	F
T	T	I	E	F
I	I	I	F	F
E	E	F	E	F
F	F	F	F	F

Таблица 3.4. Истинностная дизъюнкция в логике L_dmin

x1y	T	I	E	F
T	T	T	T	T
I	T	I	T	I
E	T	T	E	E
F	T	I	E	F

Таблица 3.5. Спорная конъюнкция в логике L_dmin

x2y	T	I	E	F
T	T	T	E	E
I	T	I	E	F
E	E	E	E	E
F	E	F	E	F

Таблица 3.6. Спорная дизъюнкция в логике L_dmin

x2y	T	I	E	F
T	T	I	T	I
I	I	I	I	I
E	T	I	E	F
F	I	I	F	F

Так как введённые операции являются операциями взятия наибольшей нижней и наименьшей верхней граней бирешётки, то они коммутативны, идемпотентны, ассоциативны, дистрибутивны:

x₁y = y₁x, x₂y = y₂x, x₁y = y₁x, x₂y = y₂x, (3.9)

x₁x = x, x₂x= x, x₁x = x, x₂x = x, (3.10)

(x₁y)₁z = x₁(y₁z), (x₂y)₂z = x₂(y₂z),

(x₁y)₁z = x₁(y₁z), (x₂y)₂z = x₂(y₂z), (3.11)

(x₁y)₁z = (x₁z) ₁ (y₁z), (x₁y)₁z = (x₁z)₁(y₁z),

(x₂y)₂z = (x₂z) ₂ (y₂z), (x₂y)₂z = (x₂z)₂(y₂z), (3.12)

Проверим законы Де Моргана для различных наборов логических связок. Для истинностного отрицания ₁ правила Де Моргана срабатывают всегда, для рефлексивного отрицания ¬₂ эти законы работают только для спорных связок (₂ и ₂), иными словами выполняются следующие соотношения:

₁(x₁y) = ₁y₁₁x, ₁(x₁y) = ₁y₁₁x

₁(x₂y) = ₁y₂₁x, ₁(x₂y) = ₁y₂₁x

¬₂(x₂y) = ¬₂y₂¬₂x, ¬₂(x₂y) = ¬₂y₂¬₂x (3.13) Прочие комбинации логических связок не подчиняются законам Де Моргана, однако после выбора иных выделенных значений логики, это может поменяться. Приведём эти соотношения:

¬₂(x₁y)  ¬₂y₁¬₂x, ¬₂(x₁y)  ¬₂y₁¬₂x

₅(x₁y)  ₅y₁₅x, ₅(x₁y)  ₅y₁₅x

₅(x₂y)  ₅y₂₅x, ₅(x₂y)  ₅y₂₅x

₄(x₁y)  ₄y₁₄x, ₄(x₁y)  ₄y₁₄x

₄(x₂y)  ₄y₂₄x, ₄(x₂y)  ₄y₂₄x (3.14)

Лемма 3.2 Композиция операций из множества {¬₂,₄,₁} позволяет построить любую нульарную функцию над L_dmin.

Доказательство.

Рассмотрим выражение

₄x₁¬₂₄¬₂x (3.15)

Его значение тождественно T при любых x, поэтому, если использовать его в качестве замены константной операции, то из леммы 3.1 вытекает, что {¬₂,₄,₁} также позволяют построить любую нульарную функцию над L_min. Лемма доказана.

Рассмотрим функции ₁(x), ₂(x), ₃(x) и ₄(x) (см. таблицу 3.7) Назовём эти функции характеристическими функциями L_dmin.

Таблица 3.7. Характеристические функции L_dmin

x	1(x)	2(x)	3(x)	4(x)
T	T	F	F	F
I	F	T	F	F
E	F	F	T	F
F	F	F	F	T

Найдем для них представление через композицию ¬₂, ₄, ₁:

₁(Х) = ₁[₁x₁¬₂₁x] = ₄¬₂₄¬₂[₄¬₂₄¬₂x₁¬₂₄¬₂₄¬₂x]

₂(Х) = ₁[₄x₁¬₂₄x] = ₄¬₂₄¬₂[₄x₁¬₂₄x]

₃(Х) = ₁[₅x₁¬₂₅x] = ₄¬₂₄¬₂[¬₂₄¬₂x₁₄¬₂x]

₄(Х) = ₁[x₁¬₂x] = ₄¬₂₄¬₂ [x₁¬₂x] (3.16)

Операция ₁(Х) имеет интересную семантику. Смысл этой операции в том, что она, фактически, переводит многозначную логику в двузначную. Можно выразить это так: «всё что не признано истиной является ложью».

Теорема 3.1. Система операций {¬₂,₄,₁} является полной системой логических операций над L_dmin

Доказательство.

Докажем по индукции. Из леммы 3.2 следует, что для любой нульарной операции теорема выполняется.

Пусть, теорема выполняется для n-арных операций, докажем, что она тогда выполняется для (n+1)-арных операций.

Рассмотрим произвольную функцию Ф(x₁,x₂,…x_n,x_n+1). Согласно индуктивному допущению Ф(x₁,x₂,…x_n,T), Ф(x₁,x₂,…x_n,I), Ф(x₁,x₂,…x_n,E), Ф(x₁,x₂,…x_n,F) выразимы при помощи композиции операций из {¬₂,₄,₁}. Обозначим эти выражения Ф₁, Ф₂, Ф₃ и Ф₄ соответственно.

Сконструируем

Ф_new = [Ф₁₁₁(х_n+1)]₁[Ф₂₁₂(х_n+1)]₁[Ф₃₁₃(х_n+1)]₁[Ф₄₁₄(х_n+1)]

Воспользовавшись соотношениями (3.4), (3.5), (3.6) и (3.13) получим:

Ф_new =₄¬₂₄¬₂ [₄¬₂₄¬₂Ф₁₁ ₄¬₂₄¬₂₁(х_n+1) ] ₁

₄¬₂₄¬₂ [₄¬₂₄¬₂Ф₂ ₁ ₄¬₂₄¬₂₂(х_n+1) ] ₁

₄¬₂₄¬₂ [₄¬₂₄¬₂Ф₃ ₁ ₄¬₂₄¬₂₃(х_n+1) ] ₁

₄¬₂₄¬₂ [₄¬₂₄¬₂Ф₄ ₁ ₄¬₂₄¬₂₄(х_n+1) ] (3.17)

Выражение Ф_new принимает значение Ф₁, если х_n+1 = T, F₂, если х_n+1 = I, Ф₃, если х_n+1 = E и Ф₄, если х_n+1 = F, иными словами Ф(x₁,x₂,…x_n,x_n+1) = Ф_new. При любых значениях х_n+1. Теорема доказана.

Лемма 3.3 Все операции системы {¬₂, ₄,₁} независимы друг от друга (не выражаются композицией остальных).

Доказательство. Очевидно, что бинарная операция ₁ не может быть представлена композицией унарных операций ¬₂ и ₄.

Операция ¬₃ не может быть представлена композицией ¬₂ и ₁. Рассмотрим все возможные представления:

x  ₄x

¬₂x  ₄x

¬₂(x₁¬₂x)=x₁¬₂x  ₄x

Все остальные представления сводимы к перечисленным трём в силу (3.4), (3.10) и (3.11).

Аналогично, операция ¬₂ не может быть представлена композицией ₄ и ₁:

x  ¬₂x

₄x  ¬₂x

₄(x₁¬₃x) = x₁₄x  ¬₂x

Все остальные представления сводимы к этим трём в силу тех же (3.4), (3.10) и (3.11).

Лемма доказана.

Следствие 3.1. Система операций {¬₂, ₄,₁} образует базис операций L_dmin.

Рассмотрим теперь различные определения операции импликации. Импликацию можно задать, как при помощи комбинации отрицания и дизъюнкции, так и независимо. Для начала рассмотрим комбинационные определения:

x₁y  ₁x₁y (3.18) x_1’y  ₁x₂y (3.22)

x₂y  ¬₂x₁y (3.19) x_2’y  ¬₂x₂y (3.23)

x₃y  ₄x₁y (3.20) x_3’y  ₄x₂y (3.24)

x₄y  ₅x₁y (3.21) x_4’y  ₅x₂y (3.25)

Полученные операции имеют различную интерпретацию, которую довольно сложно выразить вербально. Попробуем вместо этого, пойти в обратном направлении, а именно, найти различные интерпретации операций логического следствия, а затем, построить или подобрать для них формальное определение.

В классической двузначной логике импликация должна быть истинной тогда и только тогда, когда следствие всегда имеет место, если имеет место предпосылка. Если говорить в терминах семантики возможных миров, импликация истинна в тех мирах, где: либо выполняется и следствие и посылка, либо только следствие, либо ничего. Если пойти дальше, можно прийти к интерпретации с точки зрения теории множеств. Истинность любой формулы А ограничивает универсум возможных значений до некоторого множества N, и если A₁  A₂, то N₁  N₂. Так, общезначимая формула не ограничивает универсум, поэтому может являться предпосылкой только другой общезначимой, и наоборот, тождественно ложная формула имеет в качестве допустимых значений пустое множество и, поэтому, ее следствием может выступать что угодно. К сожалению, такая интерпретация становится возможной для многозначной логики, только после выбора множества выделенных значений, поэтому поговорим о ней позже.

Рассмотрим импликацию, как следствие для обоих агентов. Эта импликация эквивалентна введенной ранее импликации ₁. Её таблица истинности будет выглядеть так:

Таблица 3.8. Импликация как следствие для обоих агентов в логике L_min

х1y	T	I	E	F
T	T	I	E	F
I	T	T	E	E
E	T	I	T	I
F	T	T	T	T

Рассмотрим импликацию как следствие для первого агента и как обратное следствие для второго. Смысл такого определения проявляется в логике спора. Её таблица истинности будет выглядеть так:

Таблица 3.9. Импликация как следствие для первого агента и обратное следствие для второго агента в логике L_min

х5y	T	I	E	F
T	T	T	E	E
I	I	T	E	E
E	T	T	T	T
F	I	T	I	T

Этой операции не соответствует ни одно из определений (3.18)-(3.25). Её можно выразить следующим образом:

x₅y = ₅x₁₅y = ¬₁₅x₁₅y = ₄x₁¬₂₄¬₂y (3.26)

Дальнейшее исследование логики L_dmin продолжим с построения аппарата логического вывода.