9.3.1. Функция готовности объекта

Функция готовности определяет вероятность работоспособного состояния объекта в произвольный момент времени.

Эта функция является решением дифференциального уравнения вероятности работоспособного состояния объекта:

- для работоспособного состояния объекта в момент времени t=0 из уравнения (69) находим К_р(0)=1 и С=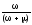, а функция готовности примет вид (рис. 37)

K_p(t)=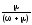+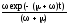=K+k exp(-(+)t); (71)

- для неработоспособного состояния объекта в момент времени t=0, K_н(0)=0 и из формулы (69) находим C=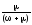, а функция готовности примет вид (см. рис. 37)

K_н(t)=k(t)=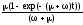=K(1-(+)t)), (72)

Функция готовности слагается из двух составляющих - переходной и установившейся (постоянной).

Установившееся значение функции готовности, являющееся асимптотой, называется коэффициентом готовности и не зависит от состояния объекта в начальный момент времени. Иначе функцию готовности называют нестационарным коэффициентом готовности.

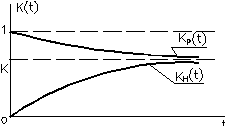
Рис. 37. Функция готовности

Функция готовности зависит и от показателя  - безотказности, и от показателя  - восстанавливаемости объекта. Значит, функция готовности является комплексным показателем надежности, характеризующим два свойства - безотказность и восстанавливаемость (ремонтопригодность).

9.3.2. Функция простоя

Функция простоя определяет вероятность неработоспособного состояния объекта в произвольный момент времени. Эта функция - решение дифференциального уравнения вероятности неработоспособного состояния объекта:

- для работоспособного состояния объекта в момент t=0 и k_p(t)=0 из формулы (70) находим C=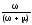, а функция простоя примет вид (рис. 38)

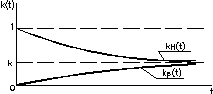
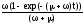k_р(t)==k(1-exp(-(+)t)); (73)

Рис. 38. Функция простоя

- для неработоспособного состояния объекта в момент t=0 и k_н(0)=1 из формулы (28) находим С=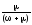, а функция простоя примет вид (см. рис. 38)

k_н(t)=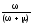+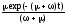=k+K exp(-(+)t). (74)

Функция простоя слагается из двух составляющих - переходной и установившейся (постоянной).

Установившееся значение функции простоя, являющееся асимптотой, называется коэффициентом простоя и не зависит от состояния объекта в начальный момент времени. Иначе функция простоя называется нестационарным коэффициентом простоя.

Функция простоя зависит и от показателя  - безотказности, и от показателя  - восстанавливаемости объекта. Таким образом, функция простоя является комплексным показателем надежности, характеризующим два свойства - безотказность и восстанавливаемость (ремонтопригодность).

9.3.3. Финальные вероятности состояний

Финальные вероятности состояний характеризуют систему в предельном стационарном режиме. Когда процесс длится достаточно долго, возникает вопрос о предельном поведении вероятностей P_i(t) при t.

Если все потоки событий, переводящие систему из одного состояния в другое, являются простейшими, т.е. стационарными (пуассоновскими) с постоянными интенсивностями _ij, то в некоторых случаях существуют финальные (или предельные) вероятности состояний,

P=lim P_i(t) (i=1,2,...,n),

t

не зависящие от того, в каком состоянии система S находилась в начальный момент времени. Это значит, что в системе S с течением времени устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятность состояний уже не меняется. В этом предельном режиме каждая финальная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии.