7.1. Дифференциальная функция нормального распределения

Дифференциальная функция (плотность вероятности) нормального распределения задается уравнением

f(x)=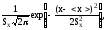 (41)

где <X> - математическое ожидание (центр рассеивания) случайной величины X; S_x - среднее квадратическое отклонение (СКО) случайной величины X.

Нормальное распределение определяется двумя параметрами:

<X> и S_x. Достаточно указать эти параметры, чтобы задать нормальное распределение.

Нормальное распределение с произвольными параметрами <X> и S_x0 называют общим.

7.1.1. Свойства дифференциальной функции нормального распределения

Дифференциальная функция нормального распределения обладает следующими свойствами:

1) функция определена на всей оси X, т.е. -X;

2) функция неотрицательна и график ее расположен над осью X, т.к. функция принимает положительные значения при всех значениях X;

3) ось X является горизонтальной асимптотой графика функции, т.к. предел функции равен 0 при неограниченном возрастании X (по абсолютной величине):

lim f(x)=0;

|x|

4) график функции симметричен относительно прямой X=<X>, т.к. в аналитическом выражении функции разность X -<X> содержится в квадрате;

5) при X=<X> функция имеет максимум

f_max=f(<x>)=;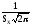

6) график функции имеет точки перегиба 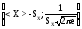и .

7.2. Правило трех среднеквадратических отклонений

Правило трех СКО состоит в том, что если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения. Вероятность того, что абсолютная величина отклонения превысит утроенное среднеквадратическое отклонение, равна 0,0027=0,27%, т.е. почти все рассеивание нормально распределенной случайной величины укладывается на интервале <X>3S_x (с точностью до долей процента).

Правило трех СКО позволяет ориентировочно определить интервал практически возможных значений случайной величины по известному математическому ожиданию или отклонение случайной величины по максимальному практически возможному отклонению от среднего значения.

7.3. Интегральная функция нормального распределения

Интегральная функция нормального распределения определяется интегрированием дифференциальной функции (41):

F(x)=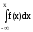=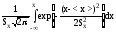. (42)

Этот интеграл не выражается через элементарные функции, но его можно вычислить через нормированную функцию, для которой есть таблица.

7.4. Нормированное нормальное распределение

Нормированное нормальное распределение позволяет составить таблицу для определения интегральной функции.

Сделаем в уравнении (42) замену переменной

=Z (43)

и приведем интеграл к виду

F(x)=F₀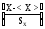=F₀(Z)=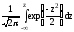. (44)

Эта замена равноценна изменению масштаба в S_x раз и смещению функции (44) вдоль оси абсцисс на величину <X> таким образом, что осью симметрии графика дифференциальной функции станет ось ординат.

Функция (44) представляет собой интегральную функцию распределения вероятностей нормально распределенной случайной величины с параметрами <X>=0 и S_x=1. Распределение с такими параметрами называется нормированным.

Из симметричности нормированного распределения относительно начала координат следует, что

F₀(-Z)=1-F₀(Z). (45)

Дифференциальная функция нормированного распределения имеет вид

f₀(Z)=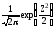. (46)

График ее симметричен относительно оси ординат, т.к. f₀(-Z)= f(Z). Функция (46) табулирована.

Из уравнений (41), (42) и (46) имеем

f(x)=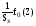=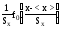. (47)

Функция (44) может быть однозначно задана таблицей, т.к. в нее не входят параметры <X> и S_x.

Таблица интегральной функции нормированного нормального распределения имеет несколько разновидностей.

1. Таблица содержит значения интегральной функции (44) нормированного нормального распределения как для положительных, так и для отрицательных аргументов.

2. Таблица содержит значения функции (44) нормированного нормального распределения только для положительных аргументов. Значения функции для отрицательных аргументов получаются по формуле (45).

3. Таблица содержит значения функции Лапласа

Ф(Z)=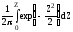. (48)

Для положительных аргументов функция Лапласа является нечетной, т.е.

Ф(-Z)=-Ф(Z). (49)

Значения интегральной функции нормированного нормального распределения получают сложением значений функции Лапласа с половиной единицы:

F(x)=F₀=F₀(Z)==+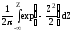

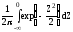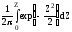+=0,5+Ф(Z)=0,5+Ф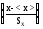. (50)

4. Таблица содержит значения разновидности функции Лапласа для положительных аргументов

Ф^*(U)=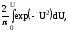

где U=.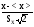

Значения функции для отрицательных аргументов определяют по формуле (49). В этом случае интегральная функция нормального распределения

F(x)=F₀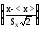^*=F₀^*(U)==

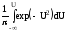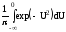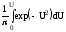=+=0,5+=

=0,5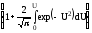=0,5[1+Ф^*(U)]=

=0,5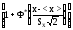. (51)

Вероятность попадания нормально распределенной случайной величины X в интервал (а,b) можно определить через интегральную функцию нормированного нормального распределения или через функцию Лапласа.

Из уравнений (44), (50), (51) имеем

P(a<X<b)=F(b)-F(a)=-=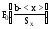

=-=-=

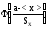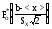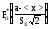=0,5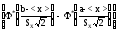. (52)

Усеченное распределение используют при конечном интервале (a,b) изменения случайной величины, в котором заключены все возможные значения.

Усеченное распределение можно рассматривать только как аппроксимацию, которая оказывается весьма точной при a  <x>--3S_x и b><x>+3S_x в соответствии с правилом трех СКО. Но при a > <x>-3S_x и b < <x>+3S_x погрешность аппроксимации становится ощутимой и функции распределения следует корректировать множителем.

Корректирующий множитель с>1 определяется из условия

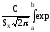
C=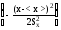dx=1,

которое выражает вероятность события, состоящего в том, что случайная величина принимает значение, принадлежащее интервалу (a,b), в котором заключены все ее возможные значения. Такое событие достоверно и вероятность его равна 1.

Интенсивность событий при нормальном распределении определяют по формуле

(x)====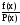

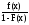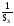
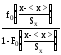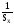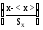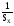=₀=₀(z),

где ₀(z)- функция интенсивности событий нормированного нормального распределения, для которой имеется таблица.

Функция интенсивности имеет горизонтальную асимптоту =0 и наклонную асимптоту 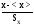=, которая пересекает ось абсцисс с координатами =0; x=<x> (рис. 26).