5.2. Безотказность объекта при параллельном соединении элементов

Безотказность системы, изображенной на рис. 20, определяется при условии, что отказ каждого элемента является случайным независимым событием.

Отказ любого элемента при параллельном соединении не приводит к отказу всей системы. Отказ системы произойдет только если откажут все параллельно соединенные элементы.

Вероятность отказа системы F_с(t) в течение времени t при параллельном соединении элементов определяется по теореме умножения вероятностей независимых событий как произведение вероятностей отказа ее элементов в течение того же времени:

F_c(t)=F₁(t) F₂(t)...F_i(t)...F_n(t)=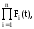 (34)

где n - число параллельно соединенных

Рис. 20. Параллельное элементов; F_i(t) - вероятность отказа i-го

соединение элементов элемента системы.

Вероятность безотказной работы сис-

темы в течение времени t при параллельном соединении элементов

P_c(t)=1- F_c(t)=1-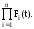 (35)

При равнонадежных элементах F_i(t)=F(t), тогда формулы (34) и (35) упрощаются:

F_c(t)=, P_c(t)=1-. (36)

Из формул (34)-(36) следует, что параллельное соединение элементов является эффективным средством повышения надежности.

Приведенные формулы справедливы только при постоянном резервировании, когда основной и резервный элементы находятся в одинаковых условиях в течение всего времени работы системы.

5.3. Безотказность объекта при смешанном соединении элементов

Безотказность объекта при смешанном соединении элементов рассчитываем по приведенным формулам для последовательного и параллельного соединения элементов. Сначала находим вероятность безотказной работы для каждой группы параллельно соединенных элементов по формулам (35) или (36), приводя систему со смешанным соединением к системе с последовательным соединением элементов. Затем определяем вероятность безотказной работы последовательно соединенных элементов по формулам (28) или (30).

6. Распределения случайных величин

6.1. Экспоненциальное распределение

Экспоненциальное (показательное) распределение определяется одним параметром . Эта особенность экспоненциального распределения является его достоинством по сравнению с распределениями, зависящими от большого числа параметров.

Параметр  - это интенсивность событий (например, отказов объектов, восстановлений работоспособности объектов). Интенсивность событий показывает среднее число событий, появившихся в единицу времени. При постоянной интенсивности событий время их появления имеет экспоненциальное распределение. И наоборот, при экспоненциальном распределении времени появления событий их интенсивность постоянна.

Время появления внезапных отказов имеет экспоненциальное распределение. Постоянная интенсивность внезапных отказов в период нормальной эксплуатации является результатом воздействия многих случайных факторов при неизменных внешних условиях. Явления изнашивания и старения объекта выражены в этом случае настолько слабо, что ими можно пренебречь.

В теории надежности экспоненциальное распределение имеют:

1) интервалы времени между событиями в простейшем потоке;

2) интервалы времени между отказами восстанавливаемых объектов в период нормальной эксплуатации;

3) длительность восстановления работоспособности объектов.

Экспоненциальное распределение является одним из распространенных в теории надежности.