2.4. Плотность распределения случайной величины

На практике при изучении непрерывных случайных величин их полученные значения делят на интервалы или разряды и подсчитывают частоты не по действительным значениям, а по разрядам.

Эмпирическое распределение - совокупность зафиксированных значений, расположенных в возрастающем порядке с указанием соответствующих частот или частостей. Эмпирическое распределение часто изображают в виде ступенчатого графика, называемого гистограммой, или в виде ломаной линии - полигона распределения (рис. 5).

При построении гистограммы по оси абсцисс откладывают интервалы х, по оси ординат - относительные частоты Q. Следовательно, высота прямоугольника равна частоте m_i (частости Q).

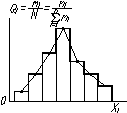
О характере распределения непрерывной случайной величины в окрестностях различных точек можно судить на основании особой функции, называемой плотностью распределения.

Рис. 5. Эмпирическое распреде- Плотность распределения

ление непрерывной случайной ве-

личины - это производная от функции распределения непрерывной случайной величины:

f(x)=.

Для дискретной случайной величины плотности распределения не существует.

Графически плотность распределения представляет собой кривую распределения непрерывной случайной величины (рис. 6).

Плотность элементарного прямоугольника, равную произведению f(x)dx, называют элементом вероятности. Для определения интегральной функции распределения необходимо вычислить площадь, ограниченную кривой f(x) и осью абсцисс в интервале от - до х. Для этого

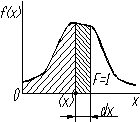
складывают все элемен- Рис. 6. График плотности распре-

ты вероятностей, заклю- деления случайной величины

ченных в данной площади от - до х:

F(x)=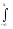f(x)dx,

где F(x) - интегральная функция распределения.

Плотность распределения характеризуется следующими основными свойствами:

1. Плотность распределения - неотрицательная функция от х, так как F(x) - неубывающая функция.

2. Площадь, ограниченная кривой f(x) и осью абсцисс (интеграл от плотности распределения в бесконечных пределах), равна единице:

f(x)dx=1.

При изучении случайных величин часто достаточно знать числовые характеристики распределения случайных величин.

3. Единичные показатели надежности объекта (епно)

3.1. Законы распределения случайной величины

Единичные показатели надежности объекта характеризуют какое-либо одно его свойство:

1) безотказность;

2) долговечность;

3) ремонтопригодность;

4) сохраняемость.

Объект в процессе хранения и эксплуатации может находиться или в работоспособном, или в неработоспособном состоянии. Время пребывания объекта в любом из этих состояний является непрерывной случайной величиной.

Как мы уже знаем, математическое описание случайных величин в теории надежности осуществляется методами теории вероятностей и математической статистики.

Универсальной вероятностной характеристикой случайной величины является закон ее распределения. Используют числовые характеристики случайной величины, то есть законы ее распределения, выражающие наиболее существенные особенности ее распределения.

В табл.2 отражена связь ЕПНО с характеристиками случайных величин. Статистическая оценка единичных показателей безотказности и долговечности проводится на модели эксплуатации (испытания) невосстанавливаемых объектов.

Модель эксплуатации невосстанавливаемых объектов

ния которых принадлежат интервалy (0,b), формула (23) примет вид

X_ср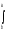.=<X>=x f(x)dx=P(x)dx. (24)

То есть математическое ожидание неотрицательной случайной величины, возможные значения которой принадлежат интервалу (0,b), численно равно площади под графиком дополнения интегральной функции (рис. 15).

По статистической информации средняя наработка до первого отказа

где t_i - наработка до первого отказа i-го объекта; N - число объектов в испытании.

Так же определяются средний

ресурс, средний срок службы, сред-

нее время восстановления работо- Рис. 15. Математическое

способности, средний срок сохра- ожидание неотрицательной

няемости. случайной величины