§ 4. Электродинамика в четырехмерных обозначениях

В гл. 18, § 6, мы уже сталкивались с оператором Даламбера, хотя и не знали, что он так называется. Мы нашли там дифферен­циальное уравнение для потенциалов, которое в новых обозна­чениях выглядит так:

(25.21)

С правой стороны (25.21) стоят четыре величины , j_x, j , j_z, поделенные на ₀ — универсальную постоянную, одинаковую во всех системах координат, если во всех системах для измере­ния заряда используется одна и та же единица. Таким обра­зом, четыре величины /jе₀, j_х/₀, j_y/₀, j_z/₀ тоже преобразуются как четырехвектор. Их можно записать в виде j_z/е₀. Оператор Даламбера не изменяется при переходе к другим системам коор­динат, так что четыре величины , А_х, А_у и A_z тоже должны преобразоваться как четырехвектор, т. е. должны быть компо­нентами четырехвектора. Короче говоря, величина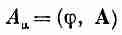

есть четырехвектор. То, что мы называли скалярным и вектор­ным потенциалами, оказывается только разными частями от од­ной и той же физической величины. Они неотделимы друг от друга. А если это так, то релятивистская инвариантность мира очевидна. Вектор А_ мы называем четырехмерным потенциалом (4-потенциалом).

В четырехмерных обозначениях (25.21) приобретает очень простой вид:

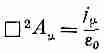
(25.22)

Физика этого уравнения та же, что и уравнений Максвелла. Но есть своя прелесть в том, что можно переписывать их в столь элегантной форме. Впрочем, эта красивая форма содержит и кое-что более значительное — из нее непосредственно видна ин­вариантность электродинамики относительно преобразований Лоренца.

Напомним, что уравнение (25.21) можно получить из урав­нений Максвелла только тогда, когда наложено дополнитель­ное условие градиентной инвариантности:

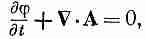
(25.23)

что означает просто A =0, т. е. условие градиентной инвари­антности говорит, что дивергенция четырехмерного вектора А равна нулю. Это требование носит название условия Лоренца. Такая форма его записи очень удобна, ибо она инвариантна, а поэтому уравнения Максвелла во всех системах отсчета сохра­няют вид (25.22).

§ 5. Четырехмерный потенциал движущегося заряда

Теперь выпишем законы преобразования, выражающие  и А в движущейся системе через  и А в неподвижной, хотя неяв­но мы уже говорили о них. Поскольку А = (, А) является четырехвектором, это уравнение должно выглядеть подобно (25.1), за исключением того, что t нужно заменить на , а x — на А. Таким образом,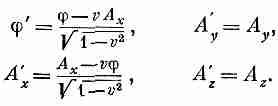

(25.24)

При этом предполагается, что штрихованная система координат движется по отношению к нештрихованной со скоростью v в направлении оси х.

Рассмотрим один пример плодотворности идеи 4-потенциала. Чему равны векторный и скалярный потенциалы заряда q, движущегося со скоростью v в направлении оси х! Задача очень упрощается в системе координат, движущейся вместе с заря­дом, ибо в этой системе заряд покоится. Пусть заряд находится в начале координат системы S', как это показано на фиг. 25.2.

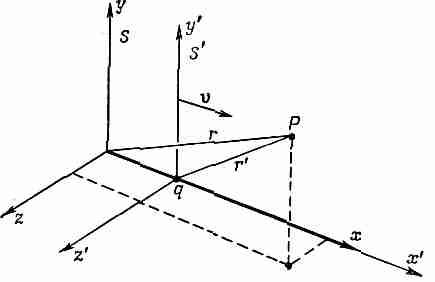
Фиг. 23.2. Система отсчета S' движется со ско­ростью v (в направлении оси х) по отношению к системе S.

Заряд, покоящийся в начале системы координат S', нахо­дится в системе S в точке x=vt. Потенциалы в точке Р могут быть найдены для любой системы отсчета.

Скалярный потенциал в движущейся системе задается выраже­нием

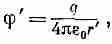
(25.25)

причем r' — расстояние от заряда q до точки в движущейся си­стеме, где производится измерение поля. Векторный же потен­циал А', разумеется, равен нулю.

Теперь без особых хитростей можно найти потенциалы  и А в неподвижной системе координат. Соотношениями, обрат­ными к уравнениям (25.24), будут

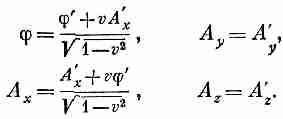
(25.26)

Используя далее выражение для '[см. (25.25)] и равенство А'=0, получаем

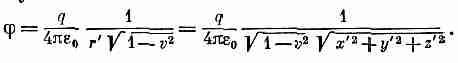
Эта формула дает нам скалярный потенциал , который мы уви­дели бы в системе S, но он, к сожалению, записан через коорди­наты штрихованной системы. Впрочем, это дело легко попра­вимо; с помощью (25.1) можно выразить t', х', у', z' через t, x, у, z и получить

(25.27)

Повторяя ту же процедуру для вектора А, вы можете показать,

что

А = v. (25.28)

Это те же самые формулы, которые мы вывели в гл. 21, но там они были получены другим методом.