Глава 25

ЭЛЕКТРОДИНАМИКА

В РЕЛЯТИВИСТСКИХ ОБОЗНАЧЕНИЯХ

§ 1. Четырехвекторы

§ 2. Скалярное произведение

§ 3. Четырехмерный градиент

§ 4. Электродинамика в четырехмерных обозначениях

§ 5. Четырехмерный потенциал движущегося заряда

§ 6. Инвариантность уравнений электродинамики

В этой главе с=1

Повторить: гл. 15 (вып. 2) «Специ­альная теория от­носительности» ; гл. 16 (вып. 2) «Релятивистская энергия и им­пульс»;

гл. 17 (вып. 2} «Пространство - время»; гл. 13 (вып. 5) «Магнитостатика»

§ 1. Четырехвекторы

В этой главе мы рассмотрим применение спе­циальной теории относительности к электроди­намике. Мы изучали теорию относительности довольно давно (гл. 15—17, вып. 2), поэтому я здесь коротко напомню основные идеи.

Экспериментально установлено, что законы физики при равномерном движении не изме­няются. Если вы находитесь внутри звездо­лета, летящего с постоянной скоростью по пря­мой линии, то не можете установить самого фак­та движения корабля: для этого надо выглянуть наружу или по крайней мере провести какие-то наблюдения, связанные с внешним миром. Лю­бой написанный нами истинный закон физики должен быть сформулирован так, чтобы этот факт природы был «встроен» в него.

Соотношение между пространством и време­нем в двух системах координат (одна из которых 6" равномерно движется относительно другой 5 в направлении оси х со скоростью v) опреде­ляется преобразованиями Лоренца

(25.1)

Законы физики должны быть таковы, чтобы после преобразований Лоренца они в новой фор­ме выглядели абсолютно так же, как и раньше. Это в точности напоминает принцип независи­мости законов физики от ориентации нашей системы координат. В гл. 11 (вып. 1) мы видели, что способом математического описания этой инвариантности относительно вращения являет­ся запись уравнений в векторном виде.

Там мы обнаружили, что если, скажем, взять два вектора

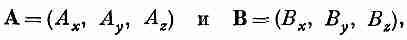
то комбинация

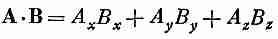
при повороте системы координат не меняется. Таким образом, если с обеих сторон уравнения мы видим скалярное произведе­ние, подобное А•В, то уравнение будет иметь в точности ту же форму в любой повернутой системе координат. Кроме того, мы открыли оператор (см. гл. 2)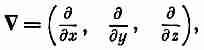

который, будучи применен к скалярной функции, дает три вели­чины, преобразующиеся в точности как вектор. С помощью это­го оператора был определен градиент, а в комбинации с дру­гими векторами — дивергенция и лапласиан. И, наконец, мы обнаружили, что, составляя суммы некоторых попарных произ­ведений компонент двух векторов, можно получить три вели­чины, которые ведут себя подобно новому вектору. Мы назвали это векторным произведением двух векторов. Используя затем векторное произведение с оператором V, мы определили ротор вектора. В дальнейшем нам часто придется ссылаться на то, что было нами сделано в векторном анализе, поэтому все важнейшие векторные операции в трехмерном пространстве, которые использовались в прошлом, мы собрали в табл. 25.1.

Пользуясь ею, можно так записать любое уравнение физики, что обе его части преобразуются при вращениях одинаковым образом. Если одна его часть — вектор, то вектором должна быть и другая часть, и обе они при вращении системы коор­динат изменяются в точности одинаково. Аналогично, если одна часть скаляр, то скаляром должна быть и другая часть, так что ни та, ни другая не изменяется при вращении системы координат и т. д.

В теории относительности пространство и время неразде­лимо связаны друг с другом, поэтому то же самое придется про­делать и для четырех измерений. Мы хотим, чтобы наши уравне­ния оставались неизменными не только при вращениях, но и при переходе в любую инерциальную систему. Это означает, что наши уравнения должны быть инвариантными относительно преобразований Лоренца (25.1). Цель настоящей главы — пока­зать, как этого можно добиться. Но прежде чем начать, примем соглашение, которое значительно облегчит нашу ра­боту (и к тому же поможет избежать путаницы). Заключается оно в таком выборе единиц измерения длины и времени, чтобы скорость света с оказалась равной единице. Вы можете считать, например, что в качестве единицы времени взят интервал, за который свет проходит отрезок в один метр (это составляет около 3•10^-9 сек). Можно даже так и назвать эту единицу вре­мени: «один световой метр». Использование этой единицы еще ярче оттеняет симметрию пространства и времени. Кроме того, из наших релятивистских уравнений исчезнут все с. (Если это почему-либо вас смущает, то вы можете в любом уравнении вос­становить их или заменить каждое t на ct, а еще лучше вставить с повсюду, где это необходимо для правильной размерности уравнения.) Теперь, после такой подготовки, мы можем дви­нуться дальше.

Наша программа состоит в том, чтобы повторить в четырех­мерном пространстве-времени все то, что мы делали с векто­рами в трех измерениях. Дело это нехитрое — мы просто будем действовать аналогично. Единственное затруднение встретится только при обозначениях (символ вектора у нас уже занят трех­мерными векторами), и несколько изменятся знаки в скалярном произведении.

Прежде всего, по аналогии с векторами в трехмерном про­странстве, введем четырехвектор как набор четырех величин a_t, а_х, а_у и а_z, которые при переходе в движущуюся систему коор­динат преобразуются подобно t, x, у и z. Для обозначения четырехвектора используется несколько различных способов. Мы же будем писать просто а_, понимая под этим группу четырех ве­личин (a_t, a_x, a_y, a_z); другими словами, значок  принимает ка­кое-либо из четырех «значений»: t, x, у и г. Иногда нам будет удобно обозначать три пространственные компоненты в виде трехмерного вектора, т. е. писать a_=(a_t , а).

Мы уже сталкивались с одним таким четырехвектором, со­стоящим из энергии и импульса частицы (см. гл. 17, вып. 2). В наших новых обозначениях он запишется так:

p_=(Е, p), (25.2)

т. е. четырехвектор p_ состоит из энергии Е и трех компонент трехмерного импульса частицы р.

Похоже, что игра действительно оказывается нехитрой: единственное, что мы должны сделать,— это найти для каждого трехмерного вектора недостающую компоненту и получить четырехвектор. Однако все же эта задача потруднее, чем кажется на первый взгляд. Возьмем, например, вектор скорости с компонентами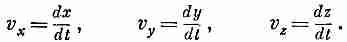

Что будет его временной компонентой? Инстинкт подсказывает нам, что поскольку четырехвектор подобен t, x, у, z, то времен­ной компонентой как будто должно быть

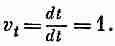
Но это неверно. Дело в том, что время t в каждом знаменателе не инвариантно при преобразованиях Лоренца. Числитель имеет правильное поведение, a dt в знаменателе портит все дело: оно не одинаково в двух различных системах.

Оказывается, что четыре компоненты «скорости», которые нам нужно выписать, превратятся в компоненты четырехвектора, если мы попросту поделим их на (1-v²). В правильности этого можно убедиться, взяв четырехвектор импульса

(25.3)

и поделив его на массу покоя, которая в четырехмерном прост­ранстве является скаляром. Мы получим при этом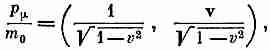

(25.4)

что по-прежнему должно быть четырехвектором. (Деление на скаляр не изменяет трансформационных свойств.) Так что четырехвектор скорости v_ можно определить так:

(25.5)

Это очень полезная величина; мы можем теперь написать, например,

(25.6)

Таков типичный вид, который должен иметь правильное реляти­вистское уравнение: каждая сторона его должна быть четырехвектором. (В правой части стоит произведение инварианта на четырехвектор, которое по-прежнему есть четырехвектор.)