1.2.5. Формула Муавра

Была найдена А.Муавром в 1707; современная её запись предложена Л. Эйлером в 1748.

zⁿ=rⁿe^in=rⁿ( cos n + i sin n). (3)

Формула (3) доказывается индукцией по n.

Умножение комплексных чисел

При она, очевидно, верна. Предположим, что она верна для некоторого n, докажем ее для n+1. Имеем:

, ч.т.д.

Для заданного найдем , удовлетворяющее уравнению . Другими словами, найдем корень n-ой степени из комплексного числа. Имеем rⁿe^in=e^i n=+2k, kZ, r= откуда получаем формулы

,

которые используются для вычисления корня n-ой степени из комплексного числа . Процесс нахождения корня n – ой степени из комплексного числа z можно описать следующим образом. Если это число не равно 0, то таких корней будет ровно n. Все они будут являться вершинами правильного n – угольника, вписанного в окружность радиуса . Одна из вершин этого многоугольника имеет аргумент, равный .

Пример. Вычислить . В этом случае , поэтому принимает три значения:

.

Рис. 1.7

Замечание: Знаки сравнения меньше, больше (<, >) не определены в C.

1.3. Верхняя и нижняя грани множества действительных чисел

Ограниченность и грани множества.

1.3.1.Ограниченное множество. Точные грани

Ограниченное сверху множество E: b xE : x  b.

b - верхняя грань множества: xE:x  b.

Ограниченное снизу множество: a xE : x  a.

a - нижняя грань множества: xE : x  a.

Точная верхняя грань множества: b = sup E – это число, удовлетворяющее двум свойствам:

1) (b - верхняя грань) xE : xb.

2) ( нет меньшей) >0  xE: x > b-.

Аналогично определяется точная нижняя грань a = inf E. Ограниченное множество E: b xE: .

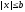Замечание: Если b = sup E, то -b = inf E , где E- зеркальное к E множество, E={xR:(-x)E}.

1.3.2.Существование точной верхней грани у ограниченного сверху множества

Теорема 1. У непустого, ограниченного сверху множества существует точная верхняя грань.

Доказательство: Пусть b верхняя грань множества E и aE. Обозначим через [a₁,b₁] отрезок 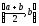, если в нем есть точки из E. В противном случае через [a₁,b₁] обозначим отрезок

Рис. 1.8

Отметим свойства этого построенного отрезка:

1) xE: x  b₁.

2) E[a₁,b₁]   .

Эту процедуру повторим для [a₁,b₁], и т. д. В результате получим последовательность вложенных отрезков [a_k,b_k], удовлетворяющих свойствам:

1)xE: x  b_k .

2) E[a_k,b_k]   .

Доказательство этого проводится по индукции. Предположим, что построен отрезок [a_k,b_k] с указанными свойствами. Разделим его пополам точкой . Через [a_k+1,b_k+1] обозначим тот из отрезков , который имеет непустое пересечение с E. Если оба содержат

Рис. 1.9

точки из E, то [a_k+1,b_k+1] пусть будет правый отрезок . Полученный отрезок обладает свойствами 1), 2). Длины этих отрезков b_k - a_k=(b - a)/2^k стремятся к 0, поэтому существует единственное число c общее для всех этих отрезков. Это число является точной верхней гранью данного множества. Действительно:

1. xE: x  c.

Предположим противное: xE:x>c, возьмем , для него существует тогда , откуда следует b_n < x, что противоречит условию x[a_n,b_n].

Рис. 1.10

2)    xE: x  c - .

Для любого  существует n: b_n - a_n <  . Выберем какое либо x[a_n,b_n] . В силу свойства 1) будет выполнено x < c, кроме того

c-x b_n - a_n <  . Таким образом, найдено требуемое x.

Рис. 1.11

Аналогично можно доказать, что у непустого ограниченного снизу множества существует точная нижняя грань.

Теорема 2. Точная верхняя грань (если она существует), единственна.

Доказательство: Пусть имеются две точных грани b₂ , b₁, b₁<b₂. Возьмет  = b₂ - b₁ > 0. По определению точной верхней грани (для b₂)  xE: x > b₂ -  = b₁, что противоречит тому, что b₁ верхняя грань.

Рис. 1.12

Замечание. Аналогично доказывается, что точная нижняя грань единственна.

Если E не ограничено сверху, то пишут sup E = +, аналогично, если E не ограничено снизу, то пишут inf E = -.